1. STATISTICA DESCRIPTIVA: Tipuri de variabile
Parametri descriptivi

Tipuri de variabile, organizarea datelor si reprezentarea lor grafica

Tipuri de variabile

Thorndike afirma ca "tot ceea ce exista se gaseste într-o anumita cantitate". McCall merge mai departe afirmând ca "tot ce se gaseste într-o anumita cantitate poate fi masurat".

Prin variabila se întelege o anumita categorie care a fost cuantificata sau masurata. Cea mai întâlnita clasificare a lor, împarte variabilele în patru tipuri: nominale (categoriale), ordinale, de tip interval si de tip raport. Primele doua tipuri sunt calitative, ultimele doua cantitative (numerice).

Scalele nominale reprezinta un prim mod de masurare a variabilelor. Presupune o categorizare a variabilei fara a indica o anumita ordine ori cantitate. Variabila sex: masculin vs. feminin; Starea civila: casatorit, divortat, vaduv, necasatorit; reprezinta exemple de scala nominala. Ele pot fi notate cu cifre (0-feminin; 1-masculin) însa acestea nu pot fi procesate în termeni de cantitate sau ordine.

Scalele ordinale sunt tot calitative. În acest caz, numerele sunt ierarhii si exprima locul sau ordinea într-un sir de date. Un exemplu banal este locul ocupat de cineva la o competitie anumita (primul, al doilea, …, ultimul). În acest caz, numerele pot fi comparate între ele în termeni de "mai mult, mai putin sau egal". Trebuie însa subliniata valoarea ordinala a numerelor. Daca un subiect ocupa locul doi, nu putem spune ca el este la egala distanta între locul unu si locul trei. Sa luam exemplul unui student care a obtinut 9,80 la examenul de admitere si a ocupat locul al doilea. Locul unu ar fi ocupat de un alt student care a avut media de 9.85, în timp ce pe locul trei s-a situat o persoana cu media 9.30. În cazul datelor ordinale, diferenta numerica în clasament nu este necesar egala cu diferenta numerica exprimata în unitatea de masura utilizata în acel caz (cinci sutimi, respectiv cincizeci de sutimi).

Cele doua tipuri de masuratori amintite pâna acum presupun întotdeauna utilizarea unor teste statistice neparametrice.

Un al treilea tip de scala este de interval. Acest tip de masuratoare permite comparatia dintre date. Diferenta dintre doua rezultate 4 si 2 este egala cu diferenta dintre 6 si 4. În cazul unui test de inteligenta diferenta între 100 IQ si 50 IQ este egala cu diferenta dintre 100 IQ si 150 IQ. Deficienta majora a acestei scale este ca valorile respective nu pot fi multiplicate sau divizate. Astfel noi nu putem concluziona ca un subiect care a obtinut 150IQ este de 1,5 ori mai inteligent decât un altul care a obtinut 100IQ si nici de 3 ori mai inteligent decât unul care a obtinut 50IQ.

Cele mai multe instrumente psihometrice sau educationale implicate în masurarea variabilelor cognitive sau comportamentale se gasesc la aceste trei nivele (nominale, ordinale, de interval).

Un ultim tip de masuratori sunt scalele de raport. Acestea poseda toate calitatile unei scale de interval si are în plus doua noi. Permite multiplicarea sau divizarea datelor (2 kg sunt jumatate din 4kg si dublul unui kg). Acest tip de masurare indica de asemenea valoarea zero absolut, ce arata lipsa totala a cantitatii masurate. Cele mai multe caracteristici fizice (greutate; înaltime; timp de reactie; nivelul adrenalinei) pot fi masurate astfel.

Ultimele doua tipuri de scale (de interval, respectiv de raport) sunt expresii cantitative ale variabilelor care pot fi supuse analizei statisticii parametrice cu mici exceptii.

Pentru a aplica tehnicile de statistica parametrica în cazul variabilelor masurate prin scale numerice (de interval sau de raport) trebuie sa vedem daca:

În plus, unele metode parametrice necesita conditii suplimentare.

Daca conditiile sunt îndeplinite, este de preferat sa utilizam tehnicile parametrice (cantitative) deoarece sunt mai solide. Aceasta înseamna cresterea sansei de a respinge o falsa ipoteza nula.

 

Organizarea datelor

Datele variabilelor pot fi prezentate fie simplu, fie grupat. Primul tip de organizare consta în stabilirea frecventei de aparitie a fiecarei valori. Pentru aceasta este necesara o ierarhizare initiala a valorilor în functie de marimea lor.

Sa presupunem ca au fost obtinute urmatoarele date ale variabilei studiate:

X = (7, 5, 7, 8, 4, 9, 8, 10, 5 3, 8, 10, 8, 7, 9, 6, 4, 7, 6, 1, 8, 6, 8, 7, 5, 7, 4, 7, 1, 9, 5, 8, 6, 7, 7). În total sunt 35 de date strânse.

Pentru a organiza datele utilizând o distributie simpla a frecventei sunt necesari urmatorii pasi:

  1. Se cauta valorile extreme din sirul de date (valoarea cea mai mare si cea mai mica);
  2. Se scriu toate valorile cuprinse între cele doua extreme într-o ordine descendenta pe o coloana;
  3. Se numara de câte ori apare fiecare valoare în sirul de date;
  4. Se trece apoi în tabel, frecventa de aparitie a fiecarui numar.

În cazul de fata vom avea:

Valoarea X

Frecventa f

1

2

2

0

3

1

4

3

5

4

6

4

7

9

8

7

9

3

10

2

                     N=35

Acest tip de grupare a datelor poate fi utilizata la fel de eficient si în cazul datelor de tip categorial sau ordinal.

De exemplu, la întrebarea unui psiholog preocupat de reclamele comerciale care sunt caracteristicile produselor pe care clientii le pretuiesc cel mai mult s-au primit 20 de raspunsuri:

X = (calitatea, pretul, cantitatea, calitatea, pretul, calitatea, pretul, pretul, pretul, utilitatea, calitatea, pretul, utilitatea, utilitatea, cantitatea, pretul, calitatea, calitatea,pretul, pretul).

Tabelul distributiei caracteristicilor produsului:

Caracteristica (x)

Frecventa (f)

Cantitate

2

Calitate

6

Utilitate

3

Pret

9

                              N=20

Mult mai utilizata, este gruparea datelor pe intervale. Pentru aceasta vom tine cont de distributia grupata a datelor, fiind necesara împartirea valorilor în clase de intervale egale. Exista doua metode principale de împartire a datelor pe intervale.

Prima este propusa de Spatz (1997) are în vedere patru pasi de urmat:

  1. Numarul de intervale trebuie sa fie între 10 si 20. Aceasta conditie are rolul de a maximiza grafic conceptul de distributie normala a datelor. Un numar mai mic de clase (intervale) conduce la o estompare grafica a distributiei normale a datelor. Un numar mai mare de 20 de intervale ne apropie de distributia grafica simpla, eliminând câstigul realizat de gruparea datelor.

  2. Stabilirea marimii intervalului (notat cu i). Trei sau cinci constitue marimea cel mai des întâlnita a intervalelor. Daca un i de 5 produce mai mult de 20 de clase, atunci se trece la o marime a intervalului superioara, de obicei 10 sau un multiplu de 10. Exista si cazuri în care este nevoie de un interval i=2 pentru a pastra minimul de 10 intervale.

  3. Primul interval începe cu o valoare multiplu de i ales. De exemplu, daca 22 este cel mai mic rezultat, iar marimea intervalului este 3, atunci vom începe cu valoarea 21 deoarece este multiplu de trei. O situatie diferita apare daca luam un i=5. În acest caz se obisnuieste sa se utilizeze o valoare de start astfel încât mijlocul intervalului sa fie un multiplu de 5. În cazul aminitit, în care 22 este cel mai mic rezultat, ar fi indicat sa se porneasca de la 18 (intervalul ar fi 18-22), iar mijlocul sau 20 (multiplu de cinci).

  4. Desi, se porneste de la valorile mici în stabilirea intervalelor, în tabel acestea sunt trecute într-o ordine descrescatoare.

Vom ordona în continuare, rezultatele a 48 de subiecti.

X = (17, 12, 8, 5, 10, 12, 23, 21, 22, 11, 14, 20, 18, 17, 15, 14, 21, 7, 10, 14, 18, 23, 25, 18, 17, 16, 29, 14, 19, 6, 27, 15, 17, 19, 14, 16, 10, 24, 17, 19, 15, 16, 12, 4, 22, 31, 19, 18).

Vom parcurge urmatorii pasi:

  1. Notam valorile extreme (4 si 31)
  2. Calculam diferenta dintre cele doua valori = 27
  3. Stabilim marimea intervalului astfel încât sa obtinem între 10 si 20 de intervale. Daca împartim 27 la 5 vom obtine 5,4 intervale, fapt de nedorit deoarece este prea departat de numarul intervalelor dorite (10-20). Daca împartim 27 la o alta marime (i=3) vom obtine 9 intervale. Deoarece patru (cea mai mica valoare) nu este multiplul lui trei va trebui sa începem de la valoarea trei (chiar daca aceasta nu exista), ca urmare distanta dintre valorile extreme se va mari cu o unitate si va deveni 28. Împartind din nou 28 la trei vom obtine 9,33, o valoarea care ne lasa noua posibilitatea de a alege între o distributie cu 9 clase sau una cu 10.
  4. Vom alege distributia cu 10 intervale, tinând cont de recomandarea autorului acestui algoritm, ca minumul intervalelor sa fie 10.
  5. Sa începe de la capatul de jos al tabelului (de la valorile mai mici). În cazul de fata vom porni de la trei, ca multiplu al marimii intervalului i=3) si vom scrie intervalele gasite. În coloana a doua a tabelului vor fi trecute valorile centrale ale intervalelor. Toate intervalele sunt egale în marime însa pot diferi în ce priveste frecventa. Fiecare interval începe cu o valoare divizibila cu marimea intervalului (i=3).
  6. Se calculeaza frecventa de aparitie a tuturor valorilor cuprinse într-un interval si le trecem în tabel în coloana trei.

Intervalul (I)

Mijlocul clasei

Frecventa (f)

30-32

31

1

27-29

28

2

24-26

25

2

21-23

22

6

18-20

19

9

15-17

16

11

12-14

13

8

9-11

10

4

6-8

7

3

3-5

4

2

O a doua posibilitate de a grupa datele pe intervale pleaca de la o formula matematica propusa de Sturges:

[Image]

 Unde: i este lungimea recomandata a intervalului;

          Xmax si Xmin sunt extremele valorilor sirului de date ordonate în ordine descrescatoare.

          lg n este logaritm zecimal din numarul de date a sirului (volumul esantionului).

Dupa cum se observa în acest caz marimea intervalulelor nu depinde numai de amplitudine (Xmax-Xmin), ci si de numarul de subiecti.

În cazul problemei date vom avea:

I = (31-4) / 1+3,322*lg 48 = 4,10

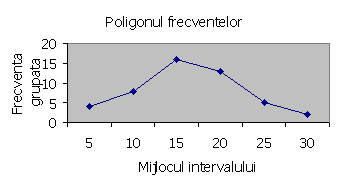
În aceasta situatie este recomandabila utilizarea unui interval cu o lungime de 4 sau 5 unitati (i = 4 sau 5). Se obisnuieste utilizarea intervalelor a caror lungime are o valoare impara pentru a usura gasirea centrului intervalului. Ca urmare, utilizând formula lui Sturges la aceleasi exemplu, vom obtine în loc de zece intervale, doar sase, deoarce am ales un interval i=5. Mijlocul intervalului este astfel ales încât sa pastreze propietatea de a fi multiplu al marimii intervalului (în cazul dat multiplu de cinci). Distributia frecventelor datelor grupate în acest caz este:

Intervalul (i)

Mijlocul clasei

Frecventa (f)

28-32

30

2

23-27

25

5

18-22

20

13

13-17

15

16

8-12

10

8

3-7

5

4

                                           N= 48

Indiferent de modalitatea pe care o alegem pentru împartirea datelor pe intervale, putem calcula si frecventa cumulata.

Frecventa cumulata a unei clase este egala cu suma frecventelor din clasa respectiva si frecventele din toate clasele cu valori inferioare. Astfel, pentru cazul de fata în cea de a doua situatie vom avea:

Intervalul (i)

Mijlocul clasei

f grupata

f cumulata

28-32

30

2

48 (2+46)

23-27

25

5

46 (5+41)

18-22

20

13

41 (13+28)

13-17

15

16

28 (16+12)

8-12

10

8

12 (8+4)

3-7

5

4

4

 

Reprezentarea grafica a datelor

Desenele din statistica se numesc grafice. Acestea sunt modalitati imagistice de reprezentare a datelor, fiind cu atât mai sugestive si mai utile cu cât numarul de date colectate creste.

Exista mai multe tipuri de reprezentare grafica. Noi vom aborda urmatoarele forme grafice adecvate statisticii descriptive: poligonul frecventelor, histogramele - pentru variabile cantitative de tip interval ori rapoarte; histogramele si cercurile de tip "placinta" - pentru variabile calitative, nominale.

Poligonul frecventelor

Este un grafic utilizat în cazul variabilelor cantitative. Un poligon al frecventelor presupune doua axe (una orizontala Ox-abscisa, alta verticala Oy-ordonatata). Pe abscisa sunt trecute clasele (intervalele) ori direct valorile sirului de date. Pe ordonata sunt trecute frecventele grupate sau simple, corespunzatoare fiecarei clase (valori).

Utilizând un sir de date prezentat anterior (n=48) care a fost împartit în prealabil în 6 clase, vom obtine urmatorul poligon al frecventelor ca reprezentare grafica a sirului de date.

Histogramele

Acest tip de grafic poate fi utilizat pentru variabile exprimate atât cantitativ cât si calitativ.

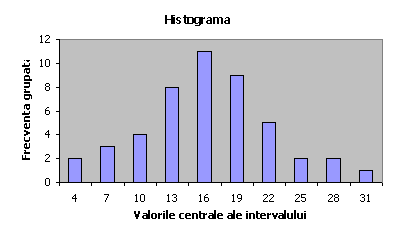
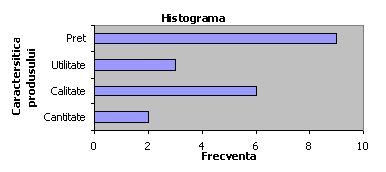
Diferenta dintre cele doua tipuri de histograme consta în faptul ca pentru datele cantitative sunt trecute pe ordonata frecventele grupate, în timp ce pentru datele calitative frecventele sunt specificate paralel cu abscisa. Pe baza exemplelor date, vom construi doua histograme (una pentru date cantitative – sirul de date împartit în 10 clase; cealalta pentru date calitative – sirul de date prezentat în cazul psihologului intersat de publicitate.

 

Graficul "placinta"

În cazul datelor calitative se utilizeaza frecvent un alt tip de reprezentare grafica sub forma unui cerc "placinta" – în engleza "pie".

Pentru exemplul dat în ce priveste caracteristicile produselor luate în considerare de catre cumparatori vom avea:

PROBLEME

  1. Numiti cele patru tipuri de variabile prezentate.
  2. Stabiliti tipul de variabila în urmatoarele cazuri:

    a) 107 – IQ b) masculin c) 24 ani d) 70 ms

    e) foarte bine; f) 0,4 depresie; g) admis; h) 51%

  3. Reprezentati histograma pentru urmatoarele date statistice:

    Xi

    f

    41-60

    25

    61-80

    39

    81-100

    48

    101-120

    33

    121-140

    19

  4. Reprezentati cercurile – placinta pentru urmatoarele date:

    PDSR

    38%

    PD

    10%

    CDR

    15%

    PRM

    9%

    PNL

    10%

    Altele

    18%

  5. Reprezentati grafic într-un alt mod datele problemei 4.

  6. Zece subiecti sunt pusi sa recunoasca autorii unor melodii prezentate timp de 5 sec. Sapte din ei identifica corect pe Adriano Celentano, doi afirma ca este vorba de Toto Cutugno, iar cel de-al zecelea crede ca este Eros Ramazotti. La final se verifica cât de siguri sunt de raspunsul lor. Scala de raspuns este de la 1 (nu sunt sigur deloc), la 5 (sunt foarte sigur). Identificati tipul de variabile prezente în acest studiu.

  7. Grupati urmatoarele numere pe intervale folosind algoritmul lui Spatz:

    41

    12

    17

    19

    21

    26

    23

    25

    14

    17

    21

    24

    29

    33

    37

    35

    19

    27

    26

    26

    26

    13

    16

    27

    29

    32

    31

    36

    30

    27

    26

    25

    28

    27

    26

    18

    25

    23

    22

    24

    21

    20

    28

    24

    27

    21

    20

    25

    26

  8. Stabiliti tabelul de distributie a frecventelor pentru urmatoarele profesiuni - Psiholog (Ps), Logoped (L), Asistent Social (A), Consilier (C), Psihopedagog (Pp):

Ps, L, L, L, A, A, C, C, C, C, C, C, Pp, Pp, Pp, Pp, Pp.

I. TEHNICI STATISTICE: Statistica descriptiva, Studiul corelational, Metode de comparatie, Tabele, Formule si raspunsuri la intrebari, Bibliografie recomandata
II. APLICATII STATISTICE: Baze de date - Exemple
III. TESTE
IV. LINK-URI RECOMANDATE

PAGINA DE START