Tehnicile ANOVA

Utilizarea testelor t este o metoda foarte buna de determinare a diferentelor dintre doua grupe. Totusi, deseori, cercetatorii lucreaza cu mai mult de doua grupe. În acest caz este nevoie de o noua metoda pentru a determina diferentele între grupe.

Tehnicile analizate în acest capitol sunt:

• ANOVA simpla;
• ANOVA cu masuratori repetate;
• ANOVA factoriala.

Înainte de a trece la prezentarea primei tehnici vom analiza mai întâi avantajele teoretice si de ordin statistic pe care le poseda analiza dispersionala (ANOVA) fata de testul t.

Vom aduce drept exemplu legea Yerkes-Dodson în ce priveste relatia dintre motivatie si învatare. Se cunoaste ca exista un optimum motivational care determina performante crescute. Daca nivelul motivational al subiectilor este prea mic ori prea puternic, rezultatul va fi acelasi: o scadere a performantei în învatare, în primul caz datorat submotivarii, în celalalt datorita supramotivarii.

Daca un experimentator decide sa aplice testul t pe doua grupe de subiecti (puternic, respectiv slab motivati) pentru a urmarii efectul motivarii asupra performantelor în învatare va ajunge la concluzia ca motivatia nu influenteaza eficienta învatarii doarece nu exista diferente semnificative între grupul subiectilor puternic motivati si grupul celor slab motivati.

Daca însa introduce o a treia grupa de subiecti care au un nivel mediu de motivare (apropiat de optimum motivational), se va observa ca performantele la învatare vor creste. Iata graficul aceastei situatii:

Se observa ca acest design experimental constituit din trei grupe este mai fidel decât cel format din doua grupe, deoarece reuseste sa surprinda faptul ca eficienta învatarii creste la un nivel mediu de motivare si scade în situatiile extreme. Acest fapt nu ar fi putut fi surprins daca am fi utilizat doar doua esantioane.

Ca urmare, cu cât numarul de grupe comparative este mai mare, cu atât se diversifica si gradele unei variabile independente. Astfel, putem observa care este efectul variabilei independente asupra celei dependente în situatii variate (lipsa ei, prezenta ei slaba, într-o masura medie sau puternica).

Pentru a creste siguranta relatiei dintre o variabila independenta si una dependenta se recomanda cresterea numarului de grupe experimentale.

Cel de-al doilea neajuns al testelor t în cazul designului experimental cu mai mult de doua grupe este de ordin statistic.

Tipul de eroare de ordinul I este determinat de formula:

Unde: a este nivelul de încredere pentru fiecare test t efectuat; c este numarul de teste t ce trebuie efectuate.

Daca exista doar doua grupe de subiecti se aplica un singur test t între grupul 1 si grupul 2. Daca exista însa trei grupe de subiecti sunt necesare trei teste t (între grupul 1 si grupul 2; între 2 si 3; respectiv între 1 si 3). Cu cât avem un numar mai mare de grupe cu atât numarul testelor t ce trebuie efectuate creste.

Ori, nivelul de încredere maxim pâna la care putem respinge o ipoteza nula este de 0,05 (.05). Conform formulei date mai sus, acest nivel de încredere se calculeaza în functie de numarul de grupe. Daca în cazul a doua grupe aplicam un singur test t nivelul de încredere al experimentului este:

Însa începând cu situatia în care avem trei grupe trebuie aplicate mai multe teste t simultane, crescând astfel sansa de a comite o eroare de tip I.

Aceasta valoare ar fi mai mare decât maximul acceptat (0,05), ca urmare nici din punct de vedere statistic nu este recomandabila utilizarea testului t pentru mai mult de doua grupe.

Pornind de la aceasta situatie, R.A. Fisher a dezvoltat o tehnica numita analiza dispersionala sau ANOVA (care în limba engleza provine de la analysis of variance). Exista mai multe tipuri de ANOVA care vor fi discutate punctual în continuare.

ANOVA simpla

Vom utiliza aceasta tehnica în situatia în care vom avea o singura variabila independenta cu mai multe trepte (mai mult de doua trepte si implicit grupe de subiecti) si o singura variabila dependenta. Tehnica este echivalentul testului t independent.

De fapt, testul t independent este un tip special de ANOVA simpla în care sunt implicate doar doua grupe. ANOVA simpla permite evaluarea ipotezei nule între mediile a doua sau mai multe serii de date cu restrictia ca acestea sa fie trepte ale aceleiasi variabile independente. Exemplul anterior contine o variabila independenta cu trei trepte: motivare slaba, medie si puternica, respectiv o variabila dependenta, eficienta în învatare. Pot exista mai multe trepte, cu conditia sa existe o singura variabila independenta, respectiv o singura variabila dependenta.

ANOVA simpla permite compararea simultana a trei sau mai multe grupe mentinând nivelul a la valoarea dorita, de maxim 0,05.

Procedeul matematic implicat în ANOVA simpla consta în analiza dispersiei variabilei dependente. În aceasta analiza dispersia totala are doua componente: dispersia din interiorul fiecarui grup format si dispersia între mediile grupelor si marea medie (media totala fara a tine cont de grupele formate). De exemplu, subiectul X1 din grupa I abaterea fata de marea medie M este data de doua componente: abaterea lui X1 fata de media grupului din care face parte M1 (X1-M1), respectiv abaterea mediei grupului I fata de marea medie (M1-M). Prima componenta este denumita dispersia intragrup si se datoreaza fluctuatiilor esantionului ales pentru studiu, cea de a doua se numeste dispersia intergrup si apare mai ales ca urmare a influentei variabilei independente.

Deci, în ANOVA simpla totalul dispersiei provine din doua surse: intragrupal si intergrupal. Ambele surse reflecta dispersia datorata selectiei randomizate a esantionului. În plus, dispersia intergrup reflecta abaterile datorate treptelor diferite ale variabilei independente. Dispersia datorata esantionarii aleatoare se mai numeste si dispersia erorii, în timp ce dispersia datorata variabilei independente poarta numele si de dispersie adevarata.

Pentru a întelege mai bine mecanismul matematic de calculare a lui F (simbolul rezultatului obtinut prin ANOVA) vom prezenta un exemplu si algoritmul de calcul pentru ANOVA simpla.

Un cercetator doreste sa urmareasca efectul unei terapii asertive asupra stimei de sine la debilii mintali. Toti subiectii aveau un QI între 70 si 80 si au fost împartiti randomizat în trei grupe de subiecti.

Din totalul de 15 participanti au fost relizate trei grupe a câte cinci subiecti fiecare. O prima grupa a urmat o terapie individuala bisaptamânala timp de o luna de zile, cel de-al doilea grup a urmat o terapie de grup în aceleasi conditii în timp ce al treilea grup, de control, n-a urmat nici o forma de terapie.

La sfârsitul experimentului subiectii au fost testati în ce priveste nivelul stimei de sine, care în acest caz constituie variabila dependenta. Rezultatele sunt prezentate în tabelul de mai jos:

Terapie individuala			Terapie grup		Grup de control
	X	X²	X	X²	X	X²
	12	144	9	81	6	36
	10	100	7	49	7	49
	11	121	6	36	2	4
	7	49	9	81	3	9
	10	100	4	16	2	4
S X	50	514	35	263	20	102
Media	10	…	7	…	4	…

Pentru calcuarea raportului F din ANOVA simpla, cea mai usoara cale este metoda denumita ABC.

Astfel trebuie mai întâi calculate A, B si C.

A se obtine prin ridicarea la patrat a rezultatelor fiecarui subiect si apoi sumarea lor (indiferent de grupa din care face parte.

B se obtine prin suma rezultatelor tuturor subiectilor (indiferent de grupa), ridicarea sumei la patrat si apoi împartirea la numarul total de subiecti ai experimentului.

C se obtine prin suma rezultatelor subiectilor din grupa 1, ridicarea la patrat a valorii obtinute urmata apoi de împartirea la totalul de subiecti ai primei grupe.

Procedeul se repeta pentru toate grupele experimentului, în final are loc adunarea tuturor rezultatelor partiale.

Îniante de a prezenta un tabel ANOVA trebuie prezentati câtiva termeni noi.

Suma patratelor (SS) este suma abaterilor standard.

Media patratica (MS) este expresia ANOVA a dispersiei esantionului.

Media mare este media tuturor rezultatelor fara a tine cont de diferentele dintre grupe.

Se obisnuieste ca orice tabel ANOVA sa fie prezentat în felul urmator:

Dispersia	SS	df	MS	F
Intergrup	C-B	k-1	(C-B) / (k-1)	MS1/MS2
Intragrup	A-C	N-k	(A-C) / (N-k)
Totala	A-B	N-1

Nota: X- rezultatul unui subiect;

N- numarul total de subiecti din experiment;

k- numarul de grupe;

SS- suma patratelor;

df- numarul de grade de libertate;

MS- media patratica

F raportul ANOVA.

Calculând A, B si C pentru problema de fata obtinem:

A = 514+263+102= 879;

B = (50+35+20) totul la patrat / 15= 735

C = (50) la patrat / 5 + (35) la patrat / 5 + (20) la patrat / 5 = 825.

Ca urmare tabele ANOVA pentru problema de fata va arata astfel:

Dispersia	SS	df	MS	F
Intergrup	90	2	45	10,00
Intragrup	54	12	4,5
Totala	144	14

Interesul major în acest tabel îl reprezinta valoarea lui F. Aceasta vine raportata la tabelul lui F pentru nivelele de semnificatie de .05 sau .01. Tabelul lui F se utilizeaza putin diferit de cel al lui t.

Se observa ca raportul F este obtinut prin împartirea Mediei patratice (MS) intergrup la media patratica (MS) intragrup. Fiecarei medii patratice îi corespunde anumite grade de libertate. În cazul problemei date, se observa citind din tabelul sumar ANOVA ca MS intergrup are 2 df (doua grade de libertate), iar MS intragrup are 12 df.

În tabelul lui F se citeste valoarea corespunzatoare gradelor de libertate pentru intergrup (pe coloana a doua deoarece df=2) si pentru intragrup (df=12, deci linia 12). Vom observa doua valori trecute la intersectia coloanei 2 cu linia 12 (3,88 pentru un p<.05 si 6,93 pentru un p<.01).

Comparând valoarea lui F obtinuta de noi (F=10) cu valoarile trecute în tabel în functie pragul de semnificatie ales pentru a respinge ipoteza nula (3,88 pentru un p<.05 si 6,93 pentru un p<.01) observam ca F obtinut este mai mare decât valoarea lui F tabelar. Aceasta înseamna ca raportul F obtinut este semnificativ statistic, ipoteza nula este respinsa, deci exista diferente între mediile celor trei grupe.

Matematic rezultatul obtinut se scrie sub forma:

F (2,12) = 10,00, p<.05 (se citeste "F cu 2 si 12 grade de libertate are valoarea 10 si este semnificativ la nivelul de .05".

Respingerea ipotezei nule ne arata doar ca cele trei grupe nu sunt egale în ce priveste media rezultatelor variabilei dependente. Cu toate acestea, nu stim cum difera cele trei grupe între ele, daca spre exemplu, doar grupa 1 difera de grupele 2 si 3 sau daca toate difera semnificativ s.a.m.d.

Pentru a depasi acest impas, prima solutie ar fi realizarea de teste t între grupele 1 si 2, 2 si 3 sau 1 si 3. În aceasta situatie reapare problema enuntata anterior privind a . De aceea sunt necesare alte solutii care poarta numele de comparatii post hoc, efectuate dupa gasirea unui raport F semnificativ.

De asemenea, pot fi utilizate si comparatii planificate pentru a testa diferentele între grupele de subiecti, înainte de efectuarea experimentului.

OBSERVATIE: Desi în problema data numarul de subiecti din fiecare grupa a fost egal, în aplicare testului ANOVA simpla numarul de subiecti din grupe poate sa nu fie egal cu conditia respectarii unei dispersii omogene în grupe.

Omogenitatea dispersiei – o masura a asocierii

Respingerea ipotezei nule arata ca exista o diferenta semnificativa între medii. În cazul unor esantioane mari acest rezultat poate fi lipsit de aplicativitate. Situatia poate fi similara unui coeficient de corelatie r=.15 semnificativ statistic la un esantion mare însa relatia dintre cele doua variabile (r=.15) arata o slaba asociere.

O masura a marimii asocierii între variabila independenta si cea dependenta în cazul ANOVA este omogenitatea dispersiei (w ² – omega patrat). Ea indica proportia din dispersia variabilei dependente care poate fi pusa pe seama variatiei variabilei independente. Masura este similara coeficientului de determinare (r²) discutat în cadrul studiului corelational.

Formula lui omega patrat propusa de Hays (1981) este:

Înlocuind în formula datele problemei obtinem:

Formulând o concluzie asupra datelor statistice, putem spune ca treptele diferite ale variabilei independente: terapia asertiva (terapie individuala, de grup, control) influenteaza semnificativ evolutia stimei de sine. F(2, 12)= 10,00, p<.05 si raspund de o proportie însemnata din dispersie (omega patrat = 54,5%).

O alta formula simpla de calcul a lui omega patrat a fost data de Tolson (1980).

Unde N este totalul subiectilor din experiment, iar k numarul de grupe formate.

Exista câteva precautii în utilizarea lui omega patrat. Cea mai importanta dintre ele se refera la utilizarea acestei masuri în conditiile în care variabila independenta a fost atent împartita în trepte cât mai egale posibil.

Grupele realizate pe baza unor variabile cantitative ar trebui sa pastreze o distanta egala între ele. Unitatile egale de tip (2 ore, 4 ore, 6 ore) conduc la utilizarea lui omega patrat fara nici o problema. În cazul unitatilor inegale de tip (2 ore, 5 ore, 15 ore) nu este indicata calcularea omogenitatii dispersiei.

Grupele realizate pe baza unei variabile independente nominale (calitative) ar trebui sa pastreze aceasta conditie dintr-o perspectiva teoretica cât mai mult posibil. În cazul problemei noastre, cele trei trepte (tratament individual, colectiv si control) nu sunt egale din perspectiva teoretica (distanta dintre tratamentul individual si cel colectiv fiind mai mica decât cea dintre nontratament si oricare din grupele experimentale). Drept consecinta, calcularea lui omega patrat nu este recomandata, fiind realizata mai sus doar în scop pur didactic.

O alta precautie a utilizarii lui omega patrat este aceea a modificarii valorii sale în functie de treptele variabilei independente. În cazul amintit (2 ore, 4 ore, 6 ore) calcularea lui omega patrat va conduce la un rezultat diferit daca ar fi fost utilizate (3 ore, 6 ore si 9 ore).

În ciuda acestor neajunsuri, în situatia în care sunt respectate în mare conditiile amintite, omogenitatea dispersiei ne ofera informatii importante si merita calculat. Este în mod special util în cazurile în care obtinem un F semnificativ, foarte mare si are rolul de a tempera concluziile primare. Se poate obtine un omega patrat modest, chiar în situatiile în care raportul F ANOVA a iesit foarte mare. În acest caz, omogenitatea dispersiei va arata mai exact în ce masura variabila independenta este responsabila (influenteaza) dispersia variabilei dependente.

Marimea efectului

Daca în capitolul referitor la testele t indexul marimii efectului a fost notat cu d, în cazul ANOVA se noteaza cu f. Formula de calcul a lui f este:

N este numarul total de subiecti cuprinsi în experiment.

Înlocuind simbolurile cu datele problemei referitoare la efectul terapiei asertive asupra stimei de sine la deficientii mintali obtinem:

OBSERVATIE: Aceasta formula este valida numai în situatia în care numarul de subiecti din fiecare grupa este egal.

Pentru situatia ANOVA factorial, MS intergrup devine MS tratament (factor), iar MS intragrup devine MS eroare (intracelula).

Urmatorul pas, consta în interpretarea valorii gasite. Cohen (1992) propune urmatoarele valori ale lui f:

Efect slab f =.10

Efect mediu f =.25

Efect mare f =.40

Valoarea obtinuta de noi arata un efect foarte puternic, cea ce înseamna o influenta puternica a variabilei independente asupra celei dependente. Totusi, datele problemei sunt artificiale si servesc doar ca exemplu de rezolvare pentru ANOVA simpla.

ANOVA cu masuratori repetate

Daca ANOVA simpla era în analogie cu testul t independent, ANOVA cu masuratori repetate este în corespondenta cu testul t dependent.

Termenul masuratori repetate implica evaluarea unui individ de doua sau mai multe ori în ce priveste variabila dependenta.

În aceasta situatie, suma patratelor totala si implicit dispersia totala sunt împartite în trei componente: dispersia dintre indivizi; dispersia datorata variabilei independente; si dispersia reziduala.

Voi prezenta în continuare tabelul sumar pentru ANOVA cu masuratori repetate necesar în vederea aflarii lui F.

Sursa dispersiei	SS	df	MS	F
Individuala	C-B	n-1	SS/df
V.independenta	D-B	k-1	SS/df	F
Reziduala	(A-B)-[(C-B)+(D-B)]	(k-1)(n-1)	SS/df
Total		N-1

Unde: n este numarul de subiecti a unei grupe; N numarul de subiecti din experiment, iar k este numarul de repetari a testarii. F se obtine facând raportul între MS independent si MS rezidual.

Mai trebuie facute câteva precizari:

SS individual = C-B;

SS independent (adevarat, tratament) = D-B;

SS rezidual = (A-B)-[(C-B)+(D-B)];

SS total = A-B

Trebuie mai întâi calculate A, B si C.

A se obtine prin ridicarea la patrat a rezultatelor fiecarui subiect si apoi sumarea lor (indiferent de grupa din care face parte.

B se obtine prin sumarea rezultatelor tuturor subiectilor (indiferent de grupa), ridicarea sumei la patrat si apoi împartirea la numarul total de subiecti ai experimentului.

C se obtine prin sumarea rezultatelor obtinute de primul subiect pe parcursul tuturor evaluarilor (k). Procedura se repeta si pentru ceilalti subiecti supusi experimentului. Aceste rezultate partiale se aduna, iar valoarea rezultata se împarte la totalul de evaluari la care este supus un subiect.

D se obtine prin sumarea rezultatelor subiectilor din grupa 1, ridicarea la patrat a valorii obtinute. Procedeul se repeta si pentru celelalte grupe, iar rezultatele partiale obtinute se aduna, suma obtinuta se împarte în final la numarul de subiecti cuprinsi într-o grupa.

Unde: k reprezinta numarul de evaluari, implicit de grupe; N numarul de subiecti dintr-o grupa.

Pentru a usura întelegerea tehnicii ANOVA unifactoriala cu masuratori repetate vom oferi spre rezolvare urmatoarea problema.

Exemplu: Un cercetator este interesat sa observe în ce masura interactiunile sociale ale populatiei cu persoane apartinând etniei rroma vor reduce atitudinea refractara fata de acestia si vor elimina prejudecatile.

Drept urmare, sase subiecti sunt pusi sa interactioneze zilnic cu un grup de alti sase minoritari rroma, în vederea realizarii unui proiect comun timp de doua luni de zile.

Subiectilor li se aplica un chestionar validat de masurare a atitudinii fata de rromi, realizat în vederea depistarii impresiei populatiei majoritare asupra rromilor, pe o axa acceptare-respingere. Scorurile mari arata un nivel crescut de acceptare.

Subiectii sunt testati de patru ori: înainte de începerea experimentului; la o luna dupa declansarea proiectului comun, la finalizarea proiectului (dupa înca o luna); si la o luna dupa terminarea proiectului. Cum a influentat trecerea unui anumit interval de timp atitudinea fata de etnia rroma?

Ipoteza pe care o lanseaza cercetatorul este: persoanele cu cât interactioneaza mai frecvent cu cei din etnia rroma, cu atât vor avea o atitudine mai toleranta fata de acestia. Ipoteza nula a cercetarii este: M1 = M2 = M3 = M4

Rezultatele celor sase subiecti la cele patru testari sunt trecute în tabelul de mai jos:

S	Înainte		Dupa 1 luna				Dupa 2 luni				Dupa 3 luni
	x	x²	x		x²		x		x²		x		x²
1	6	36	9		81		12		144		11		121
2	8	64	10		100		14		196		15		225
3	5	25	6		36		10		100		11		121
4	7	49	9		81		9		81		10		100
5	4	16	8		64		10		100		9		81
6	9	81	6		36		11		121		10		100
S	39	271		48		398		66		742		66		748
M	6,5		8,0				11,0				11,0

Calculam mai întâi valorile A, B, C si D:

A = 271 + 398 + 742 + 748 = 2159

B = (39 + 48 + 66 + 66) la patrat / 24 = 1998,375

C = [(6 + 9 + 12 + 11)² + (8 + 10 + 14 + 15)² + (5 + 6 +10 + 11) ² + (7 + 9 + 9 + 10)² + (4 + 8 + 10 + 9)² + (9 + 6 + 11 + 10)²] / 4 = 2039,75

D = (39² + 48² + 66² + 66²) / 6 = 2089,5.

Urmatorul pas este calcularea sumei patratelor:

SS individual = C – B = 2039,75 – 1998,375 = 41,375

SS adevarata (experiment) = D–B = 2089,5 – 1998,375 = 91,125

SS reziduala = (A-B)-(C-B)+(D-B)=(2159 – 1998,375) – [(2039,75–1998,375)+(2089,5 – 1998,375)] = 28,125

SS totala = A – B = 2159 – 1998,375 = 160,625.

Sa nu uitam ca:

SS totala = SS individual+SS experiment+SS rezidual

Al treilea pas consta în calcularea gradelor de libertate:

df individual = n – 1 = 6 – 1 = 5.

df experimental = k – 1 = 4 – 1 = 3.

df rezidual = (k – 1)(n – 1) = (6 – 1)(4 – 1) = 15.

df totala = N – 1 = 24 – 1 = 23.

Penultimul pas pentru a constitui tabelul ANOVA necesita calcularea mediei patratice (MS):

MS individual = SS individual / df individual = 41,375 / 5 = 8,275.

MS experimental = SS experimental / df experimental = 91,125 / 3 = 30,375.

MS rezidual = SS rezidual / df rezidual = 28,125 / 15 = 1,875.

Ultimul pas consta în calcularea raportului lui F în cazul ANOVA cu masuratori repetate:

F = MS experimental / MS rezidual;

F = 30,375 / 1,875 = 16,2.

Iata tabelul sumar ANOVA masuratori repetate în cazul problemei date:

Sursa dispersiei	SS	df	MS	F	F,p<.05
Individuala	41,375	5	8,275
Experiment	91,125	3	30,375	16,2	3,29*
Reziduala	28,125	15	1,875
Totala	160,625	23

Dupa calcularea lui F se compara valoarea gasita cu cea prezenta în tabelul lui F. Se observa ca valoarea obtinuta F = 16,2 este mai mare decât cea prezenta în tabelul lui F la un prag de .05, pentru 3 si 15 grade de libertate (F = 3,29). Ca urmare ipoteza nula este respinsa, constatându-se diferente semnificative în ce priveste mediile celor patru serii de evaluari. Matematic rezultatul obtinut se scrie:

F (3, 15) = 16,2, p<.05.

Orice test parametric necesita îndeplinirea mai multor conditii pentru a putea fi utilizat. Voi prezenta în continuare conditiile necesare pentru a putea aplica ANOVA simpla si ANOVA cu masuratori repetate.

Asumptii ale tehnicii ANOVA simpla:

1. Esantionul a fost selectat randomizat din populatie. În cazul în care acest fapt este greu de realizat se recomanda ca masura compensatorie randomizarea subiectilor în grupele experimentale.
2. Variabila dependenta este distribuita normal. Aceasta conditie este greu de demonstrat în conditiile în care mare parte din cercetarile care utilizeaza ANOVA se realizeaza cu un numar mic de subiecti. Încalcarea acestei conditii are însa efecte reduse asupra erorii de tip
3. Dispersia subiectilor împartiti pe grupe de tratament diferite sa fie egala. Exista coeficienti special construiti pentru a observa în ce masura este realizata aceasta omogenitate a dispersiei. Testul ANOVA este o tehnica robusta, rezistenta la violarile prezentate (în special a primelor doua). Numai în cazuri deosebite în care exista violari majore a acestor conditii si mai ales a existentei unor dispersii inegale si a unor grupe de subiecti inegale se recomanda sa se renunte la testul ANOVA în favoarea utilizarii unor tehnici neparametrice.

   Asumptiile testului ANOVA cu masuratori repetate

   Primele trei conditii sunt identice. La acestea se adauga o conditie suplimentara:

4. Coeficientii de corelatie între diferitele evaluari repetate sa fie aproximativ egali.

Daca omogenitatea dispersiei si egalitatea aproximativa a coeficientilor de corelatie sunt încalcate, eroarea de tip I poate fi afectata. Totusi, se poate continua aplicarea tehnicii parametrice daca se procedeaza la aplicarea unei corectii prealabile referitoare la gradele de libertate.

Valoarea lui F obtinuta va fi comparata cu valoarea prezenta în tabelul lui F pentru (1 si n-1 grade de libertate) si nu pentru k-1 si (n-1)(k-1) grade de libertate ca în situatia în care aceste conditii erau îndeplinite.

ANOVA factoriala

Pâna în prezent am discutat cazurile de ANOVA în care era prezenta o singura variabila independenta cu mai multe trepte si o singura variabila dependenta, celelate variabile fiind controlate. Noi putem însa manipula mai mult decât o singura variabila independenta.

În acest caz de analiza dispersionala, ANOVA factorial, este vorba de studiul influentei simultane a doua sau mai multe variabile independente asupra unei variabile dependente.

Exista mai multe avantaje în utilizarea unui design experimental factorial. Un prim câstig este eficienta studiului, deoarece doua sau mai multe variabile independente sunt analizate simultan si sunt extrase informatii referitoare atât despre fiecare factor în parte, cât si despre interactiunea dintre acestia si influenta lor asupra variabilei independente.

Din aceasta perspectiva, ANOVA factorial conduce la calculul a trei teste statistice F. Doua dintre ele se realizeaza pentru a gasi efectele principale (efectul principal al variabilei A si efectul principal al variabilei B), iar cel de-al treilea test masoara efectul interactiunii AB asupra variabilei dependente. Efectele principale sunt analoage dispersiei intergrup din ANOVA simpla, iar testul interactiunii (simbolizat AB) ne arata daca rezultatele obtinute la diferite nivele ale variabilei A sunt dependente de nivelul factorului B si viceversa.

În cele ce urmeaza ne vom opri doar asupra testului ANOVA bifactorial (2 variabile independente cu mai multe trepte fiecare), fiind însa posibile si experimente care necesita mai mult de doi factori (variabile independente). Algoritmul de rezolvare a acestor situatii este asemanator cu ANOVA bifactorial, dar este prea complicat de calculat manual.

Orice ANOVA factorial are specificat designul experimental realizat, sub forma unor cifre. Un design factorial cu doua variabile, fiecare având câte trei trepte va fi notat, ANOVA 3x3, un altul în care prima variabila are doua trepte, iar cea de a doua cinci, va fi simbolizata ANOVA 2x5. Un design factorial (cu trei variabile independente), în care primele doua variabile au câte 3 trepte, iar cea de-a treia doar doua, va fi notat ANOVA 3x3x2 s.a.

Voi prezenta în continuare forma grafica a unui design experimental bifactorial, în care cele doua variabile independente au câte trei trepte.

	B1	B2	B3
A1	A1B1	A1B2	A1B3	Medie A1
A2	A2B1	A2B2	A2B3	Medie A2
A3	A3B1	A3B2	A3B3	Medie A3
	Medie B1	Medie B2	Medie B3

Dupa cum se observa, din combinarea celor doi factori fiecare cu trei trepte, se obtin noua situatii experimentale diferite. Acestea poarta numele de celule.

Daca în cazul ANOVA simpla dispersia totala era suma dispersiei intergrup cu dispersia intragrup, în cazul ANOVA factoriala exista patru surse ale dispersiei totale, si anume: dispersia intracelula (echivalenta cu dispersia intragrup); dispersia de-a lungul mediei liniilor; dispersia de-a lungul mediei coloanelor si dispersia datorata interactiunii dintre cele doua variabile independente, suma ultimeler trei fiind echivalentul dispersiei intergrup.

Din aceasta cauza sunt testate trei ipoteze nule în cazul ANOVA bifactorial. Primele doua se refera la efectul variabilelor independente luate separat (media fiecarei linii este egala, respectiv media fiecarei coloane este egala), iar cea de-a treia se refera la interactiune.

Pornind de la aceste coordonate voi prezenta tabelul sumar pentru ANOVA factorial.

Sursa disp.	SS	df	MS	F
Lin.-factorA	C-B	l-1	SS/df	F
Col.-factorB	D-B	c-1	SS/df	F
Interactiune	(E-B)-(C-B)(D-B)	(l-1)(c-1)	SS/df	F
Intracelule	(A-E)-(E-B)	(N-1)-rest	SS/df
Total	A-B	N-1

Unde: l este numarul de linii (treptele variabilei A); c este numarul de coloane (treptele variabilei B), iar gradele de libertate (df) pentru intracelule se calculeaza scazând din df total celelalte grade de libertate (linii, coloane, interactiune).

Utilizând aceasta metoda ABC în calcularea celor trei F pentru ANOVA factorial este necesar mai întâi sa calculam A, B, C, D si E.

A se obtine prin ridicarea la patrat a rezultatelor fiecarui subiect si apoi sumarea lor (indiferent de celula din care face parte.

B se obtine prin sumarea rezultatelor tuturor subiectilor (indiferent de grupa), ridicarea sumei la patrat si apoi împartirea la numarul total de subiecti ai experimentului.

C se obtine prin sumarea rezultatelor obtinute de subiectii prezenti pe linia întâi, rezultatul obtinut fiind ridicat la patrat. Procedura se repeta si pentru celelalte linii. Aceste rezultate partiale se aduna, valoarea rezultata se împarte la totalul de subiecti ai unei linii, indiferent de coloane.

D se obtine prin sumarea rezultatelor subiectilor din coloana 1 si apoi ridicarea la patrat a valorii obtinute. Procedeul se repeta si pentru celelalte coloane, iar rezultatele partiale obtinute se aduna iar suma se împarte la numarul de subiecti cuprinsi într-o coloana, indiferent de linie.

E se obtine prin sumarea rezultatelor subiectilor din celula întâi si apoi ridicarea la patrat a sumei obtinute. Procedeul se repeta pentru toate celulele designului factorial, iar rezultatele partiale obtinute se însumeaza. Rezultatul obtinut se împarte la numarul de subiecti dintr-o celula.

OBSERVATIE: Formulele date sunt aplicabile si în situatia în care celulele nu au un numar egal de subiecti, cu conditia sa nu varieze foarte mult sau sa fie proportionali. În acele situatii calculul lui C, D si E se diferentiaza înlocuind numitorul cu numarul de subiecti pentru fiecare linie, coloana sau celula în parte. De pilda, E se va calcula astfel:

Pentru a concretiza elementele teoretice prezentate în cadrul ANOVA factoriala, voi oferi drept exemplu model rezolvarea unei probleme care necesita aplicarea ANOVA factorial.

Pornind de la experimentele care au aratat ca memoria are o natura reconstructiva, un cercetator doreste sa studieze în ce masura relatarile martorilor oculari sunt influentate de întrebarile adresate si de experienta subiectilor fata de situatia în cauza, pentru a stabili gradul de încredere în depozitiile martorilor.

În experiment, cercetatorul propune subiectilor sa vizioneze un film despre un accident de circulatie. Dupa vizionare le cere subiectilor sa estimeze viteza cu care rulau masinile în momentul accidentului (variabila dependenta). El este interesat de influenta a doua variabile independente.

O prima variabila este data de manipularea experimentatorului. Astfel, el cere unui grup sa estimeze viteza cu care s-au "zdrobit" masinile; unui al doilea grup i s-a cerut acelasi lucru, dar foloseste expresia "s-au lovit", iar în a treia situatie subiectii au fost întrebati "ce viteza" aveau masinile în momentul accidentului.

Cea de a doua variabila independenta luata în calcul a fost experienta subiectiilor care a avut doua trepte: soferi si ne-soferi. Avem asadar un model de ANOVA factorial de tip 3x2 (trei linii si doua coloane).

Ipoteza cercetatorului este: relatarile subiectilor sunt influentate atât de expresiile utilizate (întrebarile anchetatorului) cât si de experienta subiectilor în situatia descrisa, în sensul ca subiectii soferi pot estima mai bine decât ne-soferii viteza de deplasare a masinii.

A = 41706;

B = 1080 la patrat / 30 = 38880;

C = (447 la patrat + 321 la patrat + 312 la patrat) / 10 = 40019,4;

D = (513 la patrat + 567 la patrat) / 15 = 38977,2;

E = (189 la patrat + 258 la patrat + 174 la patrat + 147 la patrat + 150 la patrat + 162 la patrat) / 5 = 40582,8

Dupa calcularea lui A, B, C, D si E cu ajutorul datelor din tabel, vom calcula suma patratelor pentru fiecare situatie.

SS linii (factorul A) = C-B = 40019,4-38880 = 1139,4

SS coloane (factorul B) = D-B = 38977,2-38880 = 97,2

SS linii x coloane (interactiune) = (E-B)-(C-B)-(D-B) = (40582,8-38880)-(40019,4-38880)-(38977,2-38880) = 466,2

SS intracelula = (A-B)-(E-B) = (41706-38880)-(40582,8-38880) = 1123,2

SS total = A-B = 41706-38880 = 2826

A1 Zdrobit	B1 Soferi		B2 Nesoferi		S A1(linie)= 189+258= 447 S A1²=7623+13644= 21267 Media lui A1 = 44,7
	X	X²	X	X²
	51	2601	63	3969
	45	2025	57	3249
	39	1521	51	2601
	30	900	48	2304
	24	576	39	1521
S	189	7623	258	13644
Media	37,8		51,6
A2 Lovit	42	1764	36	1296	S A2(linie)= 174+147= 321 S A2² =6192 +4401= 10593 Media lui A2 = 32,1
	39	1521	30	900
	33	1089	30	900
	33	1089	27	729
	27	729	24	576
S	174	6192	147	4401
Media	34,8		29,4
A3 Accident	33	1089	36	1296	S (linie)A3 = 150+162= 312 S A3² = 4536+5310 = 9846 Media lui A3 = 31,2
	33	1089	33	1089
	30	900	36	1296
	27	729	30	900
	27	729	27	729
S	150	4536	162	5310
Media	30		32,4
	S B1=189+174+150=513 S B1²=7623+ 6192+4536 = 18351 Media B1= 34,2		S B2=258+147+162=567 S B2²=13644 +4401+5310 = 23355 Media B2= 37,8		S Xtot.=1080 S Xtotal² = 41706 Media lui X total = 36

De asemenea putem stabili gradele de libertate:

df linii = numarul de linii(l) – 1 = 3-1 = 2

df coloane = numarul de coloane(c) – 1 = 2-1 =1

df interactiune = (l-1)(c-1) = (3-1)(2-1) = 2

df total = Numarul total de subiecti (N) – 1 = 30-1 = 29

df intracelula = df total – df linii – df coloane – df interactiune = 29-2-1-2 = 24

Având calculate atât suma patratelor (SS) cât si gradele de libertate (df) putem calcula media patratica pentru aceste elemente:

MS linii (A) = SS linii / df linii = 1139,4 / 2 = 569,7

MS coloane (B) = SS coloane / df coloane = 97,2 / 1 = 97,2

MS linii x coloane (interactiune - AB) = SS linii x coloane / df linii x coloane = 466,2 / 2 = 233,1

MS intracelula (eroare) = SS intracelula / df intracelula = 1123,2 / 24 = 46,8.

Ultimul pas ramas de facut este calcularea celor trei F:

FA = MS linii / MS intracelula = 569,7 / 46,8 = 12,17

FB = MS coloane / MS intracelula = 97,2 / 46,8 = 2,07

FC = MS interactiune / MS intracelula = 233,1 / 46,8 = 4,98

Tabelul sumar ANOVA 3x2 al problemei este:

Sursa dispersiei	SS	df	MS	F	Prag p
Linii (A)	1139,4	2	569,7	12,17 (2,24)	<.01
Coloane (B)	97,2	1	97,2	2,07 (1,24)	>.05
Interactiune	466,2	2	233,1	4,98 (2,24)	<.05
Intracelula	1123,2	24	46,8
Totala	2826	29

Asadar, se observa ca din cele trei raporturi F, doua sunt semnificative statistic F linii (determinat de factorul A) si F interactiune (determinat de actiunea comuna a factorilor A si B).

Se obisnuieste sa se reprezinte grafic influenta factorilor A si B si a interactiunii lor asupra variabilei dependente. Pe abscisa este trecuta una din variabilele independente (într-un mod arbitrar), în timp ce pe ordonata sunt trecute valorile variabilei dependente.

Vom prezenta un grafic ilustrativ utilizând datele problemei de fata.

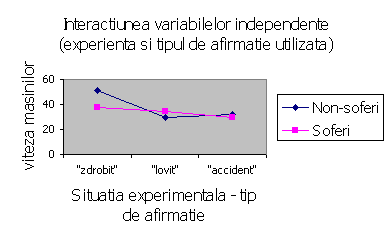
Doua variabile independente care nu interactioneaza au o reprezentare grafica de tip paralel: Dupa cum se observa în problema de fata, variabilele interactioneaza între ele, cele doua linii intersectându-se chiar în doua locuri.

Asa cum am observat si în cazul precedentelor teste ANOVA se poate calcula omega patrat ca masura a asocierii între variabilele independente si cele dependente. Existând trei raporturi F, se pot calcula trei omogenitati ale dispersiei (pentru dispersia liniilor, data de influenta factorului A asupra variabilei dependente; pentru dispersia coloanelor, data de influenta factorului B; si pentru dispersia interactiunii data de actiunea comuna a factorilor A si B asupra variabilei dependente).

Formulele de calcul a lui omega patrat sunt:

Pentru omega linii (factorul A):

Pentru omega coloane (factorul B):

Pentru omega interactiune (factorii AB):

Trebuie amintit ca aceste tehnici omega sunt utilizate doar în conditiile în care raporturile F sunt semnificative statistic. Pentru problema de fata, doar F linii (factorul A) si F interactiune (factorii A si B) au fost semnificativi si au respins ipoteza nula. Ca urmare, în problema data vor fi calculati doar doi coeficienti omega patrat.

Datele indica ca aproximativ 36,4% din dispersia estimarii vitezei automobilelor în momentul accidentului se datoreaza manipularii afirmatiilor experimentatorului, iar 12,9% poate fi atribuita interactiunii dintre cele doua variabile (estimarea vitezei depinde de interactiunea data de exprimarea cercetatorului si experienta subiectilor ca si conducatori auto).

Raporturile F stabilite în cazul ANOVA simpla, sau ANOVA cu masuratori repetate, dar si în cazul ANOVA factorial sunt denumite si teste omnibus. De la ele se porneste apoi spre analize aprofundate de comparare a datelor. Aceste analize pot avea loc atât înainte de realizarea experimentului (comaparatii a priori) cât si dupa gasirea unui F semnificativ (comparatii post-hoc). Asemenea tehnici comparative vor fi prezentate în capitolul urmator.

Asumptiile testului ANOVA factorial:

Primele trei asumptii prezentate în cazul celorlalte teste ANOVA ramân valide. La acestea se adauga altele doua:

4.Celulele trebuie sa fie independente. Aceasta înseamna ca formulele prezentate în cazul ANOVA factorial sunt valabile în cazul esantioanelor independente si sunt inadecvate în studiul esantioanelor corelate (dependente). Exista alte solutii pentru ANOVA factorial cu masuratori repetate, care însa nu sunt prezentate în aceast caiet.

5.Treptele ambilor factori sunt alese de experimentator (design factorial fix). Daca treptele sunt alese randomizat din mai multe posibilitati formulele prezentate în acest capitol nu se aplica.

PROBLEME

1. Pornind de la ideile behavioristilor, se doreste sa se vada care este efectul diferitelor tehnici comportamentale în tratarea fricii de persoanele decedate la 48 de persoane voluntare cuprinse în studiu. Acestea au fost împartite în mod aleator în 4 grupe. Grupa repartizata tehnicii in vivo a petrecut în singuratatea unui cimitir izolat o ora. O alta grupa a vizionat un film pe aceasta tema. Grupa a treia a vizionat acelasi film, dar în timpul prezentarii a fost pusa muzica relaxanta, calmanta. Ultima grupa a fost de control. Eficienta tratamentului a fost apoi evaluata printr-o scala specifica, unde rezultatele mici înseamna o frica mai redusa. Iata rezultatele celor patru grupe:

1. Stabiliti numarul de grade de libertate pentru F;
2. Stabiliti daca valoarea lui F este semnificativa statistic;
3. Interpretati rezultatele gasite;
4. Calculati omogenitatea dispersiei daca este cazul si marimea efectului;
5. Interpretati valorile gasite;
6. Reprezentati grafic valorile medii pentru fiecare grupa;
7. Utilizând informatiile din capitolul urmator dedicat tehnicilor de comparatie multipla post-hoc, stabiliti care grupe sunt semnificativ diferite de celelalte. Folosti toate tehnicile post-hoc adecvate.
8. Stabiliti daca putem infirma ipoteza nula conform careia: (Gr.1 + Gr2 +Gr.3) / 3 = Gr.4
   
   2.Stabiliti grafic designul factorial pentru cazurile:

1. Patru tipuri de scolarizare pentru trei categorii de deficiente: severe, medii, minore.
2. Trei tipuri de ADHD: impulsivi, hiperactivi si atentionali fata de doua tipuri de tratament si o grupa de control.
   
   3. Unii cercetatori au stabilit ca sexul si lateralitatea cerebrala influenteaza vârsta la care intervine decesul unei persoane.

1. Identificati care sunt variabilele independente si cele dependente;
2. Calculati SStot, SSA, SSB, SSAB, si SSeroare;
3. Stabiliti si interpretati valoarea lui F pentru fiecare situatie;
4. Calculati omogenitatea dispersiei daca este cazul si marimea efectului pentru fiecare factor si interactiune;
5. Reprezentati grafic valorile medii ale vârstei de deces;
6. Calculati efectele simple daca este cazul, daca nu utilizati o alta metoda post hoc.
   
   4. Analizati datele unui studiu longitudinal desfasurat pe o perioada de 1 an si jumatate, timp în care au avut loc patru testari, imediat dupa (0 luni), la sase luni de la terminarea programului (6 luni de la prima testare), la un an de la terminarea programului (12 luni) si la 18 luni de la finalizarea programului(18 luni). Programul în cauza a fost un pachet psiho-educational destinat reducerii absenteismului din 10 scoli. Iata rezultatele obtinute:

1. Stabiliti numarul de grade de libertate pentru F;
2. Construiti tabelul sumar ANOVA;
3. Stabiliti daca valoarea lui F este semnificativa statistic. Interpretati rezultatele gasite;
4. Calculati omogenitatea dispersiei daca este cazul si marimea efectului. Interpretati valorile gasite;
5. Reprezentati grafic valorile medii pentru fiecare grupa;
6. Utilizând informatiile din capitolul urmator dedicat tehnicilor de comparatie multipla post-hoc, stabiliti care grupe sunt semnificativ diferite de celelalte. Folosti toate tehnicile post-hoc adecvate.
7. Analizati contrastele pentru problema data daca: Ho1: M1 = M4; Ho2: M2 = M3; Ho3: M1+M4 = M2+M3
8. Realizati o analiza directionala pentru problema de fata si interpretati rezultatele obtinute.
   

I. TEHNICI STATISTICE: Statistica descriptiva, Studiul corelational, Metode de comparatie, Tabele, Formule si raspunsuri la intrebari, Bibliografie recomandata
II. APLICATII STATISTICE: Baze de date - Exemple
III. TESTE
IV. LINK-URI RECOMANDATE

PAGINA DE START
afsava@socio.uvt.ro