Studiul corelational

Corelatia este o metoda statistica utilizata pentru a determina relatiile dintre doua sau mai multe variabile. Exista mai multe tipuri de corelatii atât parametrice cât si neparametrice.

Coeficientul de corelatie este o valoare cantitativa ce descrie relatia dintre doua sau mai multe variabile. El variaza între (-1 si +1), unde valorile extreme presupun o relatie perfecta între variabile în timp ce 0 înseamna o lipsa totala de relatie liniara. O interpretare mai adecvata a valorilor obtinute se face prin compararea rezultatului obtinut cu anumite valori prestabilite în tabele de corelatii în functie de numarul de subiecti, tipul de legatura si pragul de semnificatie dorit.

Corelatii parametrice

Principalele doua conditii ce trebuie a fi îndeplinite pentru a utiliza probe parametrice sunt:

• distributia normala a variabilei de interes din cadrul esantionului cercetarii;
• omogenitatea dispersiei esntionului cercetarii referitor la variabila supusa studiului.

Probele parametrice sunt preferate în cazul îndeplinirii acestor conditii deoarece sunt mai solide, ceea ce înseamna cresterea sansei de a respinge o ipoteza falsa. Aceste conditii pot fi verificate prin localizarea mediei în cadrul distributiei normale a datelor cât si prin calcularea indicatorilor de omogenitate a esantionului cercetat.

Exista mai multe tipuri de corelatii parametrice. Pe parcursul acestui subcapitol ne vom opri la:

1.  - coeficientul de corelatie simpla (Bravais-Pearson);

2. - coeficientul de corelatie eneahoric;

3. - coeficientul de corelatie partiala;

4. - coeficientii de corelatie biserial si triserial.

Coeficientul de corelatie simpla r

În acest tip de corelatie sunt implicate doua variabile numerice care îndeplinesc conditiile parametrice. Pentru fiecare subiect avem doua rezultate. Calculul coeficientului de corelatie simpla (Bravais-Pearson) implica abaterile relative ale rezultatelor din cele doua distributii fata de mediile corespunzatoare. Exista mai multe formule de calcul în acest sens. Una din formulele de calcul a lui r este:

Unde:

N = numarul de subiecti al esantionului;

S x la patrat si S y la patrat se obtin prin ridicarea la patrat a rezultatelor si apoi sumarea lor.

S x totul la patrat si S y totul la patrat se obtin prin însumarea tuturor x-ilor si y-ilor si apoi se ridica rezultatul la patrat.

S xy este suma produselor dintre cele doua variabile.

O alta formula de calcul, porneste de la covarianta:

Unde: n este numarul de subiecti; Sx si Sy sunt abaterile standard ale celor doua variabile; Mx si My sunt mediile celor doua variabile.

Pentru o întelegere mai buna a acestor situatii vom apela la exemplul urmator: Un cercetator doreste sa stabileasca ce legatura exista între abilitatea unui individ de a fi îndragostit si altruismul sau social. Sa ne imaginam deci, ca ar exista un test prin care sa poata fi masurata cantitativ abilitatea de a fi îndragostit, proba pe care cercetatorul ar corela-o cu o scala de evaluare a gradului de altruism social. Au fost testati 20 de subiecti. Pentru usurarea calculelor se realizeaza un tabel ajutator, în care sunt trecute printre altele si valorile obtinute la testare (X= abilitatea de a fi îndragostit; Y= altruismul).

Sb	x	y	x2	y2	xy	Sb	x	Y	x2	y2	xy
1	16	20	256	400	320	11	4	11	16	121	44
2	12	17	144	289	204	12	10	14	100	196	140
3	10	14	100	196	140	13	12	15	144	225	180
4	8	9	64	81	72	14	11	17	121	289	187
5	11	12	121	144	132	15	12	14	144	196	168
6	9	10	81	100	90	16	10	13	100	169	130
7	7	13	49	169	91	17	14	19	196	361	266
8	9	12	81	144	108	18	7	15	49	225	105
9	15	20	225	400	300	19	6	8	36	64	48
10	6	10	36	100	60	20	13	18	169	324	234

S x= 202; S y= 281; S x2= 2232; S y2= 4193; S xy= 3019; (S x)2= 40804; (S y)2= 78961.

În urma rezultatelor obtinute la cele doua teste se poate calcula r simplu înlocuind în formula data mai sus:

OBSERVATII:

- Suma de x² este diferita de (x) ² ;

- Uneori apare un coeficient de corelatie negativ atunci când relatia dintre variabile este de fapt pozitiva. Conteaza modul în care sunt evaluate variabilele. Daca una din variabile implica o valoare mare la un rezultat mare, iar cealalta variabila indica o valoare mare la un rezultat mic atunci o corelatie negativa între elemente indica de fapt o asociere pozitiva între variabile.

Interpretarea încrederii lui r

Criteriul dupa care poate fi discutata semnificatia lui r presupune consultarea unei tabele special construite. Prin acest procedeu se poate respinge ipoteza nula conform careia ca nu exista o relatie adevarata (semnificativa), între variabile, iar eventualele asocieri se datoreaza întâmplarii. Daca o relatie este semnificativa din punct de vedere statistic, adica este de încredere, înseamna ca vom obtine rezultate similare daca s-ar reface experimentul.

În utilizarea tabelului lui r putem alege diferite praguri de semnificatie. Exista o întelegere la nivelul comunitatii stiintifice internationale ca pragul minim acceptat pentru a considera o relatie semnificativa statistic este 0,05. Aceste valori pot fi însa si mai mici.

Pentru aflarea semnificatiei unui coeficient de corelatie este necesara parcurgerea urmatorilor pasi:

1. Se alege nivelul de semnificatie dorit, sa zicem de 0,05. Aceasta înseamna ca la efectuarea a 100 de experimente vom obtine un rezultat bun datorat întâmplarii în maxim 5 cazuri din 100. În restul cazurilor vom obtine un rezultat bun datorita asocierii reale dintre variabile. La nivelul de 0,01 relatia este si mai puternica, iar eroarea are loc numai într-un singur caz din 100. Deci testul de semnificatie de 0,01 este mai riguros la nivelul de .01 decât la nivelul de .05 si este nevoie de o corelatie mai puternica pentru a atinge nivelul de semnificatie de 0,01.

2. Se stabileste tipul de relatie între variabile: bilaterala (two-tailed), respectiv unilaterala (one-tailed). Cercetatorul este cel care decide ce valoare va consulta. În cazul în care din punct de vedere teoretic, se urmareste sa se demonstreze ca doua variabile coreleaza fie direct, fie invers, va fi folosit testul unilateral. Daca asemenea informatii lipsesc si se doreste relevarea doar a coefientului de corelatie fara a se preciza directia legaturii, vorbim despre testul bilateral. Matematic pentru testul unilateral avem r12>0 sau r12<0, în timp ce pentru testul bilateral avem r12`0. În exemplul dat, întâlnim situatia unui test bilateral deoarece nu este precizata directia legaturii între usurinta de a se îndragosti si altruism.

3. Se citeste din tabel valoarea lui lui r pentru coloana corespunzatoare numarului de grade de libertate (notat cu df). Acestea sunt pentru r de df=N-2 stabilindu-se în functie de numarul de subiecti N validati.

4. Daca valoarea lui r obtinuta în urma calcularii sale o depaseste pe cea din tabel, atunci aceasta este semnificativa la pragul de semnificatie ales, în cazul nostru de 0,05 (notat si cu .05) si numarul de grade de libertate specificat. Se poate observa ca valoarea coeficientului de corelatie necesara pentru un r "semnificativ" scade pe masura ce creste numarul de subiecti, implicit gradele de libertate. Se remarca astfel ca valorile foarte mici ale coeficientilor de corelatie pot fi semnificative numai daca se lucreaza cu grupe mari de subiecti. Spre exemplu un r = 0,64 este semnificativ la un prag de semnificatie p<.05 pentru opt grade de libertate, adica 10 subiecti (N-2), unde în dreptul valorii de p.05 (0,05) la df=8 se gasea în tabel valoarea de 0.63 pentru testul bilateral. La fel de semnificativ este si un r = 0,20 la un prag de semnificatie p<.05 pentru df=100, coeficientul obtinut fiind mai mare decât valoarea de 0,19 tecuta în tabel.

În cazul problemei data spre exemplu am obtinut un r = 0,83 semnificativ la un parg de semnificatie p<.05 si df = 18. În tabel era trecuta valoarea de 0,44, cifra mult mai mica decât cea obtinuta de noi. Interpretarea acestui rezultat arata ca ipoteza nula este respinsa si ca exista o relatie semnificativa din punct de vedere statistic între capacitatea de a oferi dragoste si gradul de altruism social.

Daca urmarim tabelul de valori ale lui r, observam ca r obtinut (0,83) este semnificativ si la un parg de semnificatie inferior p<.001 si df = 18, în dreptul careia era trecuta în tabel valoarea de 0,67.

Interpretarea corelatiei din perspectiva semnificatiei

Statistica poate raspunde la doua întrebari privind datele pe care le avem: Sunt autentice relatiile (efectele) descoperite? Ce semnificatie au acestea?

Cel mai utilizat criteriu pentru interpretarea semnificatiei coeficientului de corelatie este coeficientul de determinare (r² – r patrat). Acest criteriu nu are întotdeauna însemnatate din cauza influentei importante pe care o are marimea lotului în determinarea coeficientului de corelatie. El trebuie analizat cu grija în cazurile în care exista un numar relativ mic de subiecti (sub 20). De asemenea, coeficientul de determinare poate fi aplicat doar daca am obtinut în prealabil un r semnificativ.

Prin intermediul lui r patrat se determina partea de asociere comuna a factorilor care influenteaza cele doua variabile. Cu alte cuvinte, coeficientul de determinare indica partea din dispersia totala a masurarii unei variabile care poate fi explicata sau justificata de dispersia valorilor din cealalta variabila.

De exemplu, în cazul problemei amintite corelatia gasita a fost de 0,83, ceea ce înseamna ca r² = (r)² (coeficientul de corelatie la patrat) este de 0,69. Uzual coeficientul de determinare se înmulteste cu 100 si exprimarea se transforma în procente din dispersie (69%).

Pentru o corelatie r de 0,83 între capacitatea de a fi îndragostit si gradul de altruism social, putem spune ca aproximativ 69% din dispersia dintr-un test este asociata cu celalalt. Urmeaza o analiza psihologica, ce ramâne la interpretarea fiecaruia atât asupra factorului comun dintre cele doua variabile cât si a diferentelor dintre ele. Un cercetator adept al teoriei triunghiulare a dragostei a lui Sternberg ar considera ca cele 69% ce implica comunalitatea celor doua variabile pot fi explicate prin doi factori: implicarea în relatie respectiv, caldura si deschiderea persoanei. Ce se poate spune despre dispersia neexplicata? În cazul problemei date este de 1 – 0,69, adica care transformat în procente înseamna 31%. Acelasi cercetator ar considera ca diferenta dintre cele doua variabile este data de lipsa pasiunii din componenta altruismului ca element definitoriu al dragostei.

Un alt cercetator ar putea explica aceste cifre pornind de la interpretarea lui Moreau data dragostei pe care o considera nu numai din perspectiva daruirii ci si din prisma schimbului avantajos reciproc.

Aceasta comunalitate dintre doua variabile sta si la baza tehnicilor de analiza factoriala.

OBSERVATIE:

Cînd utilizam coeficientul de determinare pentru a interpreta coeficientii de corelatie este nevoie de o relatie puternica (r mare) pentru a explica o parte mare din dispersia comuna. Astfel, un r de 0,71 este necesar pentru a explica jumatate din dispersia celuilalt test.

Interpretarea coeficientului de corelatie depinde în mare masura si de scopul corelatiei. De exemplu, daca analizam fidelitatea unui test este necesara o corelatie mult mai mare decît atunci când vrem sa determinam pur si simplu daca exista o relatie între doua variabile.

O corelatie de 0,90 nu este pur si simplu de trei ori mai mare decât una de 0,30; ea este de fapt de noua ori mai mare (0,30) la patrat = 0,09 sau 9% si (0,90) la patrat = 0,81 sau 81%.

Coeficientul de corelatie eneahoric

Exista cazuri în care se adopta o clasificare mai grosiera a datelor, acestea fiind grupate pentru fiecare variabila în câte trei clase. Aranjarea datelor într-un tabel va capata o înfatisare particulara în care ne intereseaza clasele extreme. În acest caz vom calcula coeficientul de corelatie eneahoric pentru un numar de 113 subiecti.

Se poate observa ca avem de a face cu doua variabile continue: agresivitatea verbala si anxietatea sociala. Pentru a surprinde mai clar corelatia dintre ele renuntam la clasele mediane care ar estompa relatia. În consecinta vom considera relatia dintre agresivitatea verbala superioara / inferioara si anxietatea sociala mare / mica.

Anx	Agres	Superior	Mediu	Inferior
Mare		18 (n1)	20	5 (n2)	A = 43
Medie		5	25	11
Mica		6 (n2)	5	7 (n3)	B = 18
		D = 29		C = 23	N = 113x

Formula lui r este:

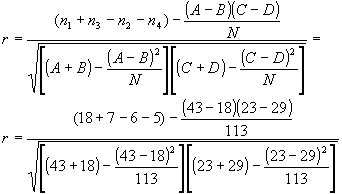
r = 0,28 la df (N-2) = 111.

Valoarea obtinuta este comparata cu valoarea din tabel a lui r de la 111 grade de libertate într-o maniera asemanatoare cu cea amintita la explicarea interpretarii semnificatiei coeficientului de corelatie r a lui Bravais-Pearson.

Coeficientul de corelatie partiala

Corelatia dintre doua variabile poate induce uneori în eroare si poate fi dificil de interpretat atunci când între cele doua variabile exista o a treia, responsabila de dependenta comuna a celor doua.

Spre exemplu, odata cu vârsta, mai multe caracteristici se modifica progresiv cum ar fi: marimea vocabularului; durata somnului; performantele mentale; gradul de activism s.a.m.d. Pe un interval mai mare de timp (spre exemplu 10 ani) corelatia dintre oricare doua variabile enumerate va fi cu certitudine puternica din cauza factorului comun de maturizare. Corelatia poate sa scada aproape de zero daca variabilitatea provocata de diferentele de vârsta este eliminata. Acest control al variabilei vârsta poate fi realizat pe doua cai: fie selectam numai copii de aceeasi vârsta, fie eliminam partial efectele statistice ale vârstei prin mentinerea constanta a acesteia. Aceasta ultima solutie presupune utilizarea corelatiei partiale.

Exista câtiva factori generali care pot influenta relatiile dintre variabile: nivelul de dezvoltare mentala; temperamentul; gradul de sanatate psihica etc. Simbolul folosit pentru coeficientul de corelatie partiala este r12.3 care semnifica o corelatie între variabilele 1 si 2 când variabila 3 este mentinuta constanta (se pot mentine oricâte variabile, simbolul devenind r12.345).

Calculul coeficientului de corelatie partiala dintre trei variabile este destul de simplu si va fi prezentat în continuare.

Corelatia dintre marimea vocabularului si durata medie de somn este un bun exemplu de corelatie falsa, fapt ce înseamna ca relatia dintre ele se datoreaza în cea mai mare parte influentei comune a unei a treia variabile (vârsta). Când efectul acestei variabile este înlaturat, corelatia dintre variabilele amintite scade sau chiar dispare. Vom nota variabilele dupa cum urmeaza: 1= marimea vocabularului; 2= numarul de ore de somn (în medie); 3= vîrsta subiectilor. Coeficientii de corelatie simpli dintre cele trei variabile au urmatoarele valori: r12= 0,80; r13= 0,90; r23= 0,88.

Formula de clacul a lui r12.3 este:

Observam ca am obtinut un coeficient de corelatie între marimea vocabularului si numarul de ore de somn aproape de zero în situatia în care influenta vârstei a fost eliminata. Initial însa, eram tentati sa credem ca între cele doua variabile exista o legatura puternica (r12= 0,80). Astfel, semnul si marimea unei corelatii partiale dintre doua variabile poate fi diferita de corelatia directa (simpla) dintre aceleasi doua variabile.

Coeficientii de corelatie biserial si triserial

Se pot ivi situatii când avem o variabila continua pusa în paralel cu o variabila discontinua (dihotomica, respectiv trihotomica). În aceste cazuri se utilizeaza un coeficient de corelatie biserial (r bis), respectiv triserial (r tris). Pentru calcularea acestor coeficienti este necesar ca N (numarul de subiecti) sa fie de peste 50.

Coeficientul de corelatie biserial

Exemplu: Un lot de 60 de profesori (învatatori) sunt testati pentru a se evalua printr-o scala experimentala atitudinea pe care o au fata de mainstreaming, ca masura benefica în vederea integrarii scolare a copiilor cu deficienta mintala. Cotele obtinute la acesta scala variaza între 10 si 50 de puncte. Variabila dihotomica consta în clasificarea profesorilor în doua clase: cei care au avut sau aveau în clasa asemenea copii si cei care nu au avut sau nu aveau în clasa copii cu deficienta mintala. S-a constatat ca 24 de profesori au lucrat cu cel putin un copil deficient mintal, iar restul de 36 de profesori nu au avut ocazia sa lucreze direct cu copii care prezentau asemenea probleme.

Media obtinuta de profesorii care au lucrat cu copiii cu deficienta mintala la atitudinea fata de mainstreaming a fost de 38,4, în timp ce profesorii care nu au lucrat cu deficienti mintali a obtinut o medie de 28,4. Abaterea standard a tuturor celor 60 de profesori supusi studiului este egala cu 8. Formula de calcul a coeficientului biserial este:

Unde: m1= media valorilor variabilei continue pentru subiectii care ating valoarea A a variabilei dihotomice (în cazul de fata cei care au lucrat cu copiii deficienti mintal);
         m2= media valorilor variabilei continue pentru subiectii care ating valoarea B a variabilei dihotomice (în acest caz cei care nu au lucrat cu copii cu deficienti mintal);
           S = abaterea standard generala pe întreg lotul de subiecti;
           pq/y = se citeste dintr-un tabel special luând ca reper fie p, fie q.

Pasi în rezolvarea problemei:

1. Se stabileste proportia (p) a celor care au lucrat cu copii cu deficienta mintala facând raportul dintre numarul acestora si totalul subiectilor din studiu. În aceeasi masura se stabileste si proportia (q) a celor care nu au lucrat cu asemenea copii.

   p= 24/60 = 0,40; q= 36/60 = 0,60;

2. Se cauta în tabel valoarea lui pq/y pentru p = 0,40 sau q = 0,60. Se observa ca valoarea lui pq/y corespunzatoare este 0,6212.

3. Se înlocuieste în formula prezentata mai sus:

Coeficientul de corelatie triserial

Când într-un studiu una din variabile este continua, iar cealalta ne apare sub forma unei clasificari trihotomice (de exemplu – bun, mediu, slab) atunci se utilizeaza pentru calculul corelatiei o formula în care m1 si m3 reprezinta mediile la variabila continua pentru cei buni si cei slabi; p1 si p3 proportia de subiecti care intra în clasa "buni", respectiv "slabi"; S este abaterea standard a distributiei complete a datelor, iar valorile rapoartelor y1/p1, respectiv y2/p2 sunt date într-un tabel special pentru calculul coeficientului de corelatie triserial luând ca reper p sau q. Se observa ca grupul celor inclusi în categoria mediu nu intra în calculele acestei formule.

Exemplu: Pornind de la problema anterioara vom împarti profesorii în trei categorii: cei care au lucrat cu copii cu deficienta mintala; cei care au lucrat cu copii cu alte deficiente dar nu si cu deficienti mintali; în sfârsit cei care nu au lucrat pâna în prezent cu copii deficienti.

În prima categorie au fost inclusi 24 profesori, a caror medie la scala de atitudine fata de mainstreaming a fost de 38,4; în a doua categorie au fost inclusi 14 profesori a caror medie a fost de 29,4, în timp ce în ultima categorie, a profesorilor care nu au lucrat niciodata cu copii cu deficienta au fost inclusi 22 de profesori care au obtinut o medie de 28,1 la scala atitudinala. Abaterea standard globala pentru toti cei 60 de subiecti a fost 8.

Pasi în rezolvarea problemei:

1. Se stabileste proportia (p1) a celor care au lucrat cu copii cu deficienta mentala facând raportul dintre numarul acestora si totalul subiectilor din studiu. În aceeasi masura se stabileste si proportia (p2) a celor care nu au lucrat cu asemenea copii, dar au lucrat cu alte categorii de deficienti, respectiv proportia (p3) a celor care nu au lucrat cu nici o categorie de deficienti.

   P1= 24/60 =0,40; p2= 14/60 =0,235; p3= 22/60 =0,365

2. Se cauta în tabel valoarea lui y1/p1 pentru p1 = 0,40 sau q1 = 0,60. Se observa ca valoarea lui y1/p1 corespunzatoare este 0,9659. La fel se cauta valoarea lui y3/p3 pentru p3 = 0,365 sau q3 = 0,635 si observam ca valoarea trecuta în tabel este 1,0289.

3. Înlocuim cifrele obtinute în formula coeficientului de corelatie triserial:

OBSERVATIE: Atât în cazul coeficientului de corelatie biserial cât si a celui triserial sunt necesare doua conditii:

• un numar de subiecti cuprinsi în esantion mai mare de 50;
• marimea claselor de subiecti luate în calcul (p1 si p2 , respectiv p1 si p3) sa fie în jurul a 33% din totalul de subiecti. În caz contrar vom obtine un rezultat distorsionat.

Rezumatul coeficientilor de corelatie parametrici:

DOUA VARIABILE CONTINUE

Date numerice continue: coeficientul de corelatie simpla;

Date numerice continue influentate de o alta variabila: coeficientul de corelatie partiala.

O VARIABILA CONTINUA SI UNA CATEGORIALA

Dihotomica: coeficientul de corelatie biserial;

Trihotomica: coeficientul de corelatie triserial.

DOUA VARIABILE CATEGORIALE

Date numerice grupate apoi pe categorii: coeficientul eneahoric.

PROBLEME

1. Descrieti printr-o fraza cum evolueaza valorile variabilelor X si Y daca între cele doua exista o corelatie directa (pozitiva). Dar daca ele ar corela negativ?

2. Ce înseamna o corelatie este semnificativa statistic?

3. Cum credeti ca vor corela urmatoarele variabile?

a) inteligenta si memorie; b) depresie si stima de sine;c)  tulburari de învatare si randamentul scolar

4. Desenati cu aproximatie norul de puncte în cazul corelatiilor: a) r = -.20 b) r = .80

5.Fie urmatoarele valori pentru variabilele: nivelul de sensibilitate corporala si gradul de anxietate.

Sensibilitate	4	6	8	7	3	5	4	5
Anxietate	10	13	14	11	8	11	9	12

1. Desenati norul de puncte;
2. Se poate calcula r simplu în cazul de fata?;
3. Stabiliti daca exista vreo asociere liniara semnificativa;
4. Calculati procentul de dispersie explicata de prezenta unui factor comun între cele doua variabile.

6.Fie urmatoarele valori pentru variabilele frica de esec (un scor mic înseamna o frica redusa) si rezultatele scolare, exprimate în media generala :

Frica de esec	Rezultate	Frica de esec	Rezultate
8	7,80	9	6,00
5	8,20	5	9,00
8	8,00	6	8,90
7	6,50	4	9,25
6	8,30	7	8,00
7	7,70	5	8,80
7	6,90	9	5,80

1. Reprezentati grafic norul de puncte corespunzator;
2. Ce puteti spune despre aceasta corelatie?;
3. Cum interpretati rezultatele gasite.
   

7. S-a descoperit ca exista o asociere între veniturile mici ale unei persoane si gradul de delicventa (r =.67). De asemenea a fost observata o legatura între gradul de delicventa si densitatea populatiei pe metru patrat (r =.58). În conditiile în care veniturile populatiei coreleaza slab cu densitatea populatiei (r =.39), stabiliti ce legatura exista între venituri si delicventa atunci când eliminam influenta variabilei densitatea populatiei.

8. Fie urmatoarele variabile: nivelul de egosintonie (de apropiere între Eul actual si cel ideal); usurinta de comunicare; si timiditatea. Toate variabilele sunt cotate astfel: valorile mici înseamna absenta sau prezenta lor în cantitate redusa, valorile mari înseamna o cantitate înseamnata.

1. Stabiliti ce asociere exista între nivelul egostintoniei si usurinta în comunicare;

2. Stabiliti gradul de asociere dintre egosintonie si usurinta în comunicare tinând constant efectul timiditatii.
3. Interpretati diferentele gasite.
   
   9. Un numar de 100 de sugari în vârsta de trei zile au fost testati aleator pentru a vedea câte secunde îsi îndreapta privirea spre doua obiecte: unul care emana un miros familiar (N=50), iar celalalt unul nefamiliar (N=50). Media primilor 50 a fost 74,1 sec, iar a celorlalti 50 a fost 64 sec. Abaterea standard a esantionului a fost 10. Determinati daca exista vreo asociere semnificativa între durata timpului de privire a obiectului si tipul de miros. Interpretati rezultatele obtinute.
   
   10.  Stabiliti daca exista vreo asociere semnificativa între declaratia subiectilor "dorm bine" vs. "dorm rau" si numarul de miscari corporale din timpul somnului. Media miscarilor pentru prima categorie este de 123, iar pentru a doua de 136, abaterea standard globala fiind 15. Au fost observati un numar de 60 de subiecti, dintre care 25 au afirmat ca au un somn bun, iar 35 s-au plâns de calitatea acestuia. Interpretati rezultatele obtinute.
   
   11. Un numar de 80 de subiecti au raspuns la un test de autoritarism. Acestia au provenit din familii cu stil educational diferit: 27 au avut parinti autoritari, 23 au avut parinti "democrati", iar 30 parinti de tip "laissez faire". Media raspunsurilor la scala de autoritarism a fost de: 8,12 pentru prima grupa, 7,60 pentru a doua grupa si 6,00 pentru cea de a treia categorie. Abaterea standard globala a fost 2. Putem afirma ca stilul autoritar al parintilor influenteaza tipul de comportament al copiilor? Pe ce va bazati raspunsul?
   
   12.Un studiu al unui institut al sanatatii doreste sa studieze daca exista vreo asociere între gradul de dizabilitate (handicap) si calitatea vietii. Ca urmare un numar de 200 de subiecti sunt evaluati utilizând un index al calitatii vietii si o scala de auto-întretinere. Rezultatele au fost grupate apoi pe trei categorii pentru fiecare variabila:

Stabiliti gradul de asociere dintre cele doua variabile. Interpretati rezultatele gasite.

I. TEHNICI STATISTICE: Statistica descriptiva, Studiul corelational, Metode de comparatie, Tabele, Formule si raspunsuri la intrebari, Bibliografie recomandata
II. APLICATII STATISTICE: Baze de date - Exemple
III. TESTE
IV. LINK-URI RECOMANDATE

PAGINA DE START
afsava@socio.uvt.ro