![[Image]](pict106.jpg)
Tehnici de comparatii multiple
În capitolul anterior, am discutat despre diferitele tipuri de analiza dispersionala (ANOVA). Am învatat cum sa respingem ipoteza nula aratând ca exista diferente semnificative între mediiile grupelor incluse în experimente.
Dupa ce ipoteza nula a fost respinsa, ramâne înca o problema de rezolvat: care combinatii de medii difera? Pentru aceasta este necesara aplicarea unor proceduri complementare de comparatii multiple, care mentin nivelul a la nivelul initial sau aproape de acesta.
Exista doua mari categorii de comparatii multiple: comparatii post-hoc (realizate dupa calcularea lui F din ANOVA), respectiv comparatii a priori (tehnici alternative ANOVA care pornesc de la alte ipoteze nule si care sunt planificate înainte de desfasurarea experimentului pe baze rationale).
Din prima categorie, vom discuta despre metodele: Tukey, Newman-Keuls, Tukey-Kramer si Scheffé, iar din a doua categorie vom discuta despre contrastele ortogonale si analiza directiei.
Pentru o mai buna structurare a lor, ele vor tratate pastrând ordinea capitolului anterior.
Proceduri de comparatie multipla în cazul ANOVA simpla si ANOVA cu masuratori repetate
Proceduri de comparatie post-hoc
Exista diferite metode post-hoc care pot fi aplicate în cazurile de ANOVA simpla si ANOVA cu masuratori repetate. Exista doua criterii dupa care sunt selectate procedeele: numarul egal de subiecti din fiecare grupa si tipul de contrast realizat. Astfel, distingem:
Metoda Tukey
Metoda Tukey, simbolizata HSD, este cel mai utilizat procedeu de comparatie multipla, denumit si testul diferentei semnificative oneste. Este conceput sa realizeze comparatii între toate perechile de medii în timp ce mentine eroarea experimentului la valorile alfa stabilite.
Ipoteza nula pentru acest test este:
Ho: Mi = Mj pentru i ¹ j
Formula de calcul a lui Q (Q analog lui F, asa cum HSD este analog ANOVA) este:
![[Image]](pict106.jpg)
Unde: Mi si Mj sunt mediile grupelor comparate;
MSintra este media patratica intragrup;
n numarul de subiecti dintr-o grupa (n1=n2).
Pentru a exemplifica aceste comparatii multiple, voi prezenta tabelul sumar a unei probleme ANOVA amintite în capitolul anterior:
Un cercetator doreste sa urmareasca efectul unei terapii asertive asupra stimei de sine la debilii mintali. Toti debilii mintali aveau un QI între 70 si 80 si au fost împartiti randomizat în trei grupe a câte cinci subiecti fiecare. Grupa 1 a fost supusa unei terapii individuale asertive, grupa 2 unei terapii de grup asertive, iar grupa 3 a fost de control (nu a primit nici un tip de terapie).
| Dispersia | SS |
df |
MS |
F |
| Intergrup | 90 |
2 |
45 |
10,00 |
| Intragrup | 54 |
12 |
4,5 |
|
| Totala | 144 |
14 |
||
| Media | Grupul 1 |
Grupul 2 |
Grupul 3 |
N |
10 |
7 |
4 |
15 |
Raportul F(2,12)=10, p<.05 arata doar ca ipoteza nula este respinsa, deci mediile celor trei grupe nu sunt egale. Care medii difera, unde se afla aceasta inegalitate (între toate mediile sau doar între media grupului 1 si 2 s.a.m.d.) nu se cunoaste din aplicarea lui F. De aceea, trebuie facute comparatii post-hoc între fiecare pereche de medii pentru a vedea unde este diferenta. Putem aplica metoda Tukey în acest sens.
Pentru a usura calculul, se recomanda ordonarea mediilor grupelor de la cea mai mica la cea mai mare. Acest pas are caracter optional în cazul metodei Tukey, însa devine obligatoriu pentru metoda Newman-Keuls.
Al doilea pas implica calcularea numitorului, care este o constanta. În cazul problemei date el se obtine astfel: radical din 4,5/5 = 0,95
Al treilea pas implica, calcularea diferentei dintre mediile respectivelor grupe.
Ultimul pas consta în împartirea diferentei dintre medii (numaratorul metodei Q) la constanta numitor calculata la pasul doi (numitorul metodei Q).
Tabel de calcul a lui Q – metoda Tukey
Grupa |
Media |
Mi-Mj |
||
| Control (3) | 4,00 | |||
| Terapie de grup (2) | 7,00 | 3,00 | ||
| Terapie individuala (1) | 10,00 | 6,00 | 3,00 | |
Q |
||||
| (3)-(2), adica 3,00 | 0,95 | 3,16 |
||
| (3)-(1), adica 6,00 | 0,95 | 6,31 |
||
| (2)-(1), adica 3,00 | 0,95 | 3,16 |
||
Valorile obtinute sunt apoi comparate cu valorile din tabel ale lui Q. Gradele de libertate ale lui Q se stabilesc tinând cont de doua aspecte (numarul de medii ce trebuie comparate si numarul de grade de libertate pentru dispersia intragrup).
În cazul problemei de mai sus exista trei medii ce trebuie comparate (m1, m2 si m3) si 12 df (N-k grupe). Valoarea tabelara pentru Q(3,12) este 3,77 la un p=.05 si 5,05 la un p=.01.
Din cele trei valori gasite de noi, doar una este mai mare decât valorile tabelare, fiind astfel semnificativa statistic (6,31). Valoarea este data de comparatia mediilor grupului 3 (terapie individuala) cu grupul 1 (control). Celelalte valori sunt mai mici decât valorile tabelare, ca urmare nu se poate spune ca diferenta înregistrata între mediile grupelor respective sunt semnificative statistic. Matematic putem spune: Q13(3,12)= 6,31, p<.01; Q12(3,12)= 3,16, p>.05; Q23(3,12)= 3,16, p>.05.
Interpretarea rezultatelor Q
Deoarece doar Q13 a avut o valoare semnificativa statistic, putem concluziona ca terapia asertiva realizata individual în cazul deficientilor mintali în vederea îmbunatatirii imaginii (stimei) de sine este mai eficienta decât lipsa oricarei terapii. În schimb, terapia asertiva de grup nu s-a dovedit eficienta, rezultatele ei fiind nesemnificative statistic în comparatie cu grupul de control. Nu au fost observate diferente semnificative nici între cele doua modalitati de terapie. Terapia individuala pare a fi modalitatea indicata în ce priveste ameliorarea stimei de sine la deficientii mintali, fiind mai buna decât lipsa oricarei interventii.
Aceste explicatii trebuie interpretate contextual. În acest caz, s-ar putea lua în considerare si numarul mic de subiecti (câte cinci în fiecare grup) care ar putea influenta rezultatele obtinute.
Testul Newman-Keuls
Are la baza ideile testului Tukey, însa presupune o analiza mai complexa. Pasii amintiti în cazul testului Tukey se pastreaza.
1. Se ordoneaza mediile grupelor de la cea mai mica la cea mai mare. Acest pas are caracter obligatoriu pentru metoda Newman-Keuls.
2. Al doilea pas implica calcularea numitorului, care este o constanta (radical din raportul dintre media patratica intragrup si numarul de subiecti dintr-o grupa). În cazul problemei date el este: v4,5/5 = 0,95
3. Al treilea pas implica, calcularea diferentei dintre mediile respectivelor grupe.
4. Urmatorul pas consta în împartirea diferentei dintre medii (pasul trei) la constanta numitor calculata (pasul doi).
La acesti pasi se adauga alti doi:
5. Se calculeaza numarul de pasi dintre medii (dupa ordonarea lor) astfel între media - 4,00 (grupa 3) si media 7,00 (grupa 2) exista doi pasi; între media 7,00 (grupa 2) si media 10,00 (grupa 1) exista tot doi pasi, însa între media 4,00 (grupa 3) si media 10,00 (grupa 1) exista trei pasi. Numarul de pasi este dat de k (numarul de grupe interpuse, incluzându-le pe cele luate în discutie).
6. Se stabilesc gradele de libertate pentru Q tabelar dupa metoda Newmans-Keuls. Daca al doilea grad de libertate ramâne identic cu cel din metoda Tukey (df intragrup), primul grad de libertate nu mai este dat de numarul de grupe, ci de numarul de pasi. Astfel Q12 si Q23 vor avea (2,12) grade de libertate, în timp ce Q13 are (3,12) grade de libertate ca si în situatia metodei Tukey, deoarece numarul de pasi este 3 (între cele doua grupe 1 si 3, se mai interpune o alta grupa (doi) cu o medie intermediara.
Drept consecinta valorile Q prin metoda Newman-Keuls, pot fi mai mici pentru grupe intermediare sau mai mari pentru grupele extreme (cu media cea mai mare, respectiv cea mai mica).
Astfel, nici valorile tabelare ale lui Q nu vor mai fi aceleasi pentru toate situatiile. Daca în cazul Q13 gradele de libertate se vor pastra si implicit valorile tabelare implicate Q(3,12) = 3,77 la un p=.05 si 5,05 la un p=.01, Q12 si Q23 se vor urmari la (2,12) grade de libertate unde valorile lui Q sunt 3,08 la un p =.05 si 4,32 la un p=.01.
Comparând din nou valorile Q obtinute cu noile valori tabelare vom observa ca toate grupele se diferentiaza semnificativ din perspectiva mediei variabilei dependente.
Q13(2,12)= 3,16, p<.05; Q23(2,12)=3,16, p<.05; Q13(3,12)= 6,31, p<.01.
Interpretarea rezultatelor Q
Se observa în urma aplicarii tehnicii Newman-Keuls ca toate mediile grupelor difera semnificativ. Astfel, se pare ca tratamentul asertiv individual de îmbunatatire a stimei de sine la deficientii mintali este o masura eficienta, fiind mai buna decât terapia asertiva realizata în grup sau decât lipsa tratamentului. De asemenea, terapia asertiva de grup se dovedeste a fi eficienta în comparatie cu absenta tratamentului, însa este mai putin eficienta în comparatie cu terapia asertiva individualizata.
OBSERVATII: Dupa cum se poate remarca, metoda Newman-Keuls este mai puternica, decelând mai multe diferente între medii decât metoda Tukey. Acest avantaj este balansat de un dezavantaj important.
Metoda Tukey pastreaza constanta eroarea experimentului la nivelul initial (spre exemplu .05), în schimb metoda Newman-Keuls mareste riscul de comitere a erorii de tip I, deoarece creste nivelul lui alfa la nivelul întregului experiment.
Daca va reamintiti aspecte discutate anterior, si anume ca nivelul de eroare a unui experiment creste odata cu numarul de grupe ale acestuia putem concluziona ca situatiile experimentale cu trei grupe sunt adecvate aplicarii atât a metodei Tukey cât si a metodei Newman-Keuls. În schimb situatiile cu patru sau mai multe grupe necesita aplicarea metodei Tukey.
O alta masura ce poate fi luata este cresterea puterii experimentului prin reducerea nivelului de probabilitate pentru respingerea ipotezei nule în cazul F de la .05 la .01 sau mai putin. În acest fel, se va evita cresterea sansei de a produce eroarea de tip I si se poate aplica metoda Newman-Keuls, indiferent de numarul de grupe.
Metoda Tukey-Kramer
Metoda este utlia pentru efectuarea de comparatii multiple în cazul grupelor inegale. Se aseamana foarte mult cu metoda Kramer pentru grupe egale, însa numitorul difera putin. Formula de calcul a lui Q utlizând Tukey-Kramer este:
![[Image]](pict107.jpg)
Unde: ni si nj reprezinta numarul de subiecti din grupele comparate, iar mi si mj mediile acestor grupe.
Numarul de grade de libertate se stabileste asemanator metodei Tukey. Primul grad de libertate este k (numarul de grupe al experimentului) iar al doilea este N-k (df pentru dispersia intragrup).
Vom contrui un exemplu ipotetic pornind de la studiul etologic a lui Hess în care s-a urmarit felul în care se realizeaza imprintingul la bobocii de rata. Acestia erau crecuti în incubator si primul lucru vazut de ei era modelul unei rate de plastic asezat pe o masa rotitoare. Hess era interesat sa identifice perioadele critice dupa nastere, când este cel mai probabil ca expunerea la model sa duca la formarea imprintingului. În acest sens au fost create patru grupe de boboci, iar timpul de expunere a bobocilor la model a fost strict controlat. Variabila independenta a fost vârsta în saptamâni la care a avut loc expunerea la model si a avut patru trepte: saptamâna 1 de viata; saptamâna 3 de viata; saptamâna 5 de viata si saptamâna 7 de viata. Variabila dependenta a fost reprezentata de numarul de secunde în care bobocii au imitat modelul si s-au rotit asemeni "mamei" lor. Iata tabelul sumar ANOVA cu date fabricate pentru a putea utiliza procedeul Tukey-Kramer.
| Sursa dispersiei | SS |
df |
MS |
F |
F .05 |
|
| Intergrup | 255,45 |
3 |
85,15 |
10,47 |
2,39 |
|
| Intragrup | 235,89 |
29 |
8,13 |
|||
| Totala | 491,34 |
32 |
||||
| Grupa | Sapt.1 | Sapt.3 | Sapt.5 | Sapt.7 | ||
| Media | 21,86 | 23,00 | 17,29 | 16,80 | N=
33 |
|
| n grupa | 7 | 9 | 7 | 10 | ||
Se observa ca valoarea lui F este semnificativa statistic, ca urmare se trece la compararea multipla a mediilor pentru a vedea care medii difera si au condus la respingerea ipotezei nule. Pentru aceasta trebuie realizati pasii amintiti si în cazul metodei Tukey.
Se ordoneaza mediile grupelor de la cea mai mica la cea mai mare. Se calculeaza numitorul pentru fiecare comparatie, deoarece numarul subiectilor din grupe nu este acelasi valoarea nu mai este o constanta.
În exemplul dat înlocuim elementele nuumitorului formulei pentru Tukey-Kramer cu datele din tabel. Pentru exemplificare vom arata calculul numitorul lui Q între grupele 1 si 2:
![[Image]](pict108.jpg)
La fel se calculeaza si ceilalti numitori si obtinem:
numitorul Q13 = 1,077
numitorul Q14 = 0,993
numitorul Q23 = 1,016
numitorul Q24 = 0,926
numitorul Q34 = 0,993
Al treilea pas implica calcularea diferentei dintre mediile respectivelor grupe. Apoi se împarte diferenta dintre medii (pasul trei) la constanta numitor calculata (pasul doi). Acesti pasi sunt prezentati în tabel:
Grupa (ordinea) |
Media |
Mi-Mj |
||
| Saptamâna 7 (4) | 16,80 | |||
| Saptamâna 5 (3) | 17,29 | 0,49 | ||
| Saptamâna 1 (1) | 21,86 | 5,06 | 4,57 | |
| Saptamâna 3 (2) | 23,00 | 6,20 | 5,71 | 1,14 |
Mi-Mj |
Numitor |
Q |
||
| (4)-(3) = 0,49 | 0,993 | 0,49 |
||
| (4)-(1) = 5,06 | 0,993 | 5,09* |
||
| (4)-(2) = 6,20 | 0,926 | 6,69* |
||
| (3)-(1) = 4,57 | 1,077 | 4,24* |
||
| (3)-(2) = 5,71 | 1,016 | 5,62* |
||
| (1)-(2) = 1,14 | 1,016 | 1,12 |
||
Valorile Q obtinute dupa metoda Tukey-Kramer vor fi comparate apoi cu valoarea din tabel a lui Q. Gradele de libertate sunt: numarul de grupe (în acest caz k=4) si gradele de libertate ale dispersiei intragrup (în acest caz N-k este 29). Valorile tabelare ale lui Q sunt 3,86 pentru p=.05 si 4,89 pentru p=.01.
Dintre valorile lui Q, se observa ca patru dintre ele sunt mai mari decât valorile tabelare ale lui Q pentru .05 (Q13, Q14, Q23, si Q24). Doua valori nu sesizeaza o diferenta semnificativa statistic între medii (Q12 si Q34).
Astfel nu se înregistreaza o diferenta în ce priveste aparitia imprintingului între prima si a treia saptamâna de viata a bobocilor. La fel nu exista diferente semnificative în evolutia acestei variabile între saptamânile 5 si 7. Ca urmare, perioada critica se înregistreaza undeva în jurul primei luni de viata, în saptamâna 4, deoarece bobocii inclusi în saptamânile 1 si 3 au obtinut rezultate superioare bobocilor carora li s-a aratat modelul mai tarziu (saptamânile 5 si 7).
De retinut ca aceasta concluzie este trasa pe baza comparatiilor a câte doua medii. Pentru a fi mai siguri ca lucrurile stau asa (imprintingul apare prin contactul bobocilor cu rata mama în prima luna de viata) este nevoie sa comparam daca mediile grupurilor "saptamâna 1" si "saptamâna 3" sunt superioare mediilor "saptamânilor" 5 si 7.
Ipoteza nula în acest caz este:
(M1+M3)/2 = (M5+M7)/2
Pentru a respinge aceasta ipoteza, este necesara o alta tehnica de comparatie multipla, metoda Scheffé.
Metoda Scheffé
Exista designuri experimentale în care cercetatorul este interesat de testarea unor ipoteze mai complexe decât simpla diferenta dintre medii. Spre exemplu, poate fi interesat daca grupele experimentale (analizate unitar) difera de grupa de control. În cazul problemei exemplu, cercetatorul vrea sa vada daca media primelor doua grupe de boboci difera de media celorlalte grupe deoarece are motive sa creada, fie din ratiuni teoretice, fie din aplicarea unor comparatii post-hoc simple, ca perioada critica de manifestare a imprintingului împarte cele patru grupe experimentale în doua: înainte de perioada adecvata aparitiei imprintingului si dupa trecerea perioadei propice imprintingului.
Cu ajutorul acestei metode se pot testa o multime de ipoteze cu o singura conditie, suma coeficientii mediilor sa fie zero.
Ipoteza pe care o vom adopta noi este valida deoarece:
(M1+M3)/2 = (M5+M7)/2 deoarece asta înseamna:
2(M1+M3) = 2 (M5+M7) adica
2M1 + 2M3 –2M5 –2M7 = 0 ceea ce înseamna ca suma coeficientilor mediilor va fi zero: 2+2-2-2 = 0
Daca am fi ales o ipoteza invalida pentru metoda Scheffé suma coeficientilor mediilor ar fi fost diferita de 0. Spre exemplu:
M1+M3 = (M5+M7)/2 adica
2M1 + 2M3 –M5 –M7 = 2 si nu zero.
Înainte de a reveni la ipoteza noastra, trebuie specificat ca în cazul în care grupele de subiecti nu sunt egale, coeficientii acestora sufera unele modificari. Adica, daca n1=n3 atunci vom scrie 1/2M1 + 1/2M3. Daca n1¹ n3 atunci acesti coeficienti nu pot avea ponderi egale si trebuie ajustati.
Coeficientul ajustat se calculeaza dupa urmatorul algoritm: se împarte volumul grupei la suma volumului celorlalte grupe cu care se asocieaza. Astfel daca n1=7; n2=9; n3=7; si n4=10, ajustarea coeficientului grupului 1 se va face în functie de subiectii grupelor saptamâna 1 si saptamâna 3 aflate în stânga relatiei de egalitate din ipoteza nula.
![]()
La fel se calculeaza si ceilalti coeficienti:
C2 = 9 / (7 + 9) = 0,57;
C3 = 7 / (7 + 10) = -0,41;
C4 = 10 / (7 + 10) = -0,59.
Coeficientii C3 si 4 au semnul minus din formula ipotezei nule, fiind situati în dreapta semnului de egalitate. Asadar daca n1=n2=n3=n4 în cazul problemei am fi avut:
0,50M1 + 0,50M3 = 0,50M5 + 0,50M7 sau
0,50M1 + 0,50M3 - 0,50M5 - 0,50M7 = 0
În problema data grupele nu sunt egale, deci vom avea:
0,43M1 + 0,57M3 = 0,41M5 + 0,59M7 sau
0,43M1 + 0,57M3 - 0,41M5 - 0,59M7 = 0
Dupa ce au fost calculati coeficientii mediilor se poate trece la calcularea valorii lui F (metoda Scheffé):
![[Image]](pict109.jpg)
Pentru problema data vom avea:
![[Image]](pict110.jpg)
F = 5,62
Aceasta valoare obtinuta este mai apoi comparata cu valoarea tabelara a lui F. Gradele de libertate pentru metoda Scheffé se stabilesc putin diferit de modul în care eram obsnuiti. Valoarea din tabel are k-1 si N-k grade de libertate, însa valoarea gasita este înmultita cu (k-1) mai apoi.
În cazul problemei date F tabelar la k-1 si N-k grade de libertate, adica (3, 29) este de 2,95 la un p=.05. Aceasta se înmulteste cu (k-1), adica cu 3 în cazul problemei date si se obtine 8,85. Aceast rezultat este comparat cu cel gasit de noi. Valoarea obtinuta este mai mica (F= 5,62), ceea ce înseamna ca ipoteza nula nu poate fi respinsa, deci nu se poate afirma ca primele doua medii apartin aceleiasi categorii, care difera de celelalte doua medii (implicit celelalte grupe).
Am putea proceda la o alta comparatie complexa utilizând aceasi metoda Schaffé pentru a observa daca nu cumva grupa 2 (bobocii care au vazut modelul în saptamâna a treia de viata) difera de celelalte grupe experimentale.
Ho: M3 - (M1+M5+M7)/3 = 0
Deoarece grupele de subiecti nu sunt egale este necesara ajustarea coeficientilor mediilor. Obtinem:
C1 (M1) = -0,29
C2 (M3) = 1
C3 (M5) = -0,29
C4 (M7) = -0,42
Coeficientii 1,3 si 4 au semn negativ deoarece ipoteza nula indica acest fapt.
Calculând F vom obtine 16,96, valoare care este superioare valorii tabelare a lui F înmultita cu k-1 (2,95*3), adica decât 8,85 la p<.05.
În acest caz se poate concluziona ca ipoteza nula este respinsa, deci bobocii din saptamâna a treia de viata au obtinut rezultate semnificativ mai bune decât bobocii din celelalte grupe. Ca urmare, se pare ca parioada de viata în jurul saptamânii a treia este cea mai propice formarii imprintingului la bobocii de rata.
Metoda Scheffé este procedeeul post-hoc cel mai conservator (sesizeaza cele mai putine diferente), însa este foarte util în situatiile în care se doreste realizarea de comparatii complexe ce depasesc nivelul perechilor de medii.
Comparatii planificate a priori
Contrastele ortogonale planificate
Prin contrast se întelege compararea de date în vederea evidentierii diferentelor dintre ele. Uneori sunt realizate asemenea comparatii înainte de realizarea efectiva a cercetarii, ca metode alternative tehnicii ANOVA prin ipotezele nule specificate.
În metoda Schaffé, era testat un contrast în ipoteza nula, deoerece suma coeficientilor lineari era zero. Contrastele ortogonale planificate constau într-un set de asemenea contraste (sistem). Numele de ortogonal vine de la fatpul ca acest set de ipoteze sunt independente si nu se influenteaza reciproc. În acest sens, nivelul lui alfa în ce priveste eroarea experimentului ramâne constanta la nivelul dorit (0,05 sau 0,01).
De exemplu, într-un studiu cu patru grupe de subiecti, un cercetator ar putea formula din ratiuni teoretice urmatoarele ipoteze:
Ho1: (M1+M2)/2 –M3 = 0
Ho2: (M1+M2)/2 – (M3+M4)/2 = 0
Ho3: M1 – M2 = 0
În acest caz coeficientii mediilor ar arata astfel:
M1 M2 M3 M4
Ho1: 1 1 -2 0
Ho2: 1 1 -1 -1
Ho3: 1 -1 0 0
Pentru a determina daca îndeplinesc criteriul contrastelor ortogonale ar trebui ca suma produselor ipotezelor sa fie tot zero.
Daca consideram ipoteza Ho1 si Ho2: suma produselor va fi: (1)*(1) + (1)*(1) + (-2)*(-1) + (0)*(-1) = 4
Aceste doua contraste nu sunt ortogonale.
Daca consideram Ho1 si Ho3 vom obtine:
(1)*(1) + (1)*(-1) + (-2)*(0) + (0)*(0) = 0.
De asemenea între Ho2 si Ho3 vom avea:
(1)*(1) + (1)*(-1) + (-1)*(0) + (-1)*(0) = 0.
Ultimele doua situatii au îndeplinit conditia impusa ca suma produsului sa fie zero.
Exista o limita a contrastelor ortogonale care pot fi generate de cercetator la începutul studiului. Ea este data de numarul de grupe din studiu si este k-1. Astfel, daca exista patru grupe de subiecti, numarul maxim de contraste va fi trei. În situatia ipotetica descrisa anterior, va trebui sa renuntam la primul contrast pentru a le pastra pe celelalte doua care îndeplinesc criteriul de ortogonalitate. De asemenea, putem renunta la al doilea contrast pentru a pastra ipotezele 1 si 3.
Drept exemplificare pentru aceasta analiza vom utiliza datele unei probleme amintite în cadrul ANOVA cu masuratori repetate.
Un cercetator este interesat sa observe în ce masura interactiunile sociale ale populatiei cu persoane apartinând etniei rroma vor reduce atitudinea refractara fata de acestia si vor elimina prejudecatile. Sase subiecti sunt pusi sa interactioneze zilnic cu un grup de alti sase minoritari rroma, în vederea realizarii unui proiect comun timp de doua luni de zile.
Subiectii sunt testati de patru ori: înainte de începerea experimentului; la o luna dupa declansarea proiectului comun, la finalizarea proiectului (dupa înca o luna); si la o luna dupa terminarea proiectului. Se urmareste daca persoanele care interactioneaza mai frecvent cu cei din etnia rroma, au o atitudine mai toleranta fata de acestia.
Tabelul sumar ANOVA în cazul problemei date:
| Sursa dispersiei | SS |
df |
MS |
F |
F, p<.05 |
|||
| Individuala | 41,375 |
5 |
8,275 |
|||||
| Experiment | 91,125 |
3 |
30,375 |
16,2 |
3,29* |
|||
| Reziduala | 28,125 |
15 |
1,875 |
|||||
| Totala | 160,625 |
23 |
||||||
| Media | Eval.1 | Eval.2 | Eval.3 | Eval.4 | ||||
| 6,5 | 8 | 11 | 11 | |||||
Sa presupunem ca cercetatorul are motive serioase sa planifice anumite ipoteze alternative ANOVA înainte de începerea experimentului. Acestea sunt:
Ho1: M1 = M4
Ho2: M2 = M3
Ho3: M1+M4 = M2+M3
Coeficientii acestor ipoteze sunt:
Ho1: 1 0 0 -1
Ho2: 0 1 -1 0
Ho3: 1 -1 -1 1
Deoarece contrastele realizate îndeplinesc toate conditia de ortogonalitate putem utiliza metoda contrastelor ortogonale a priori.De asemenea, deoarece numarul de subiecti este acelasi în fiecare grupa (n=6) nu vom proceda la ajustarea coeficientiilor mediilor.
Formula de calcul a lui F în cazul contrastelor ortogonale este:
![[Image]](pict111.jpg)
Astfel:
![[Image]](pict112.jpg)
![[Image]](pict113.jpg)
![[Image]](pict114.jpg)
Valorile F obtinute vof fi comparate cu valorile tabelare ale lui F pentru 1 si N-k grade de libertate. Spre deosebire de metoda Schaffé în care valoarea tabelara era înmultita cu k-1 înainte de compararea valorilor, în contrastele ortogonale valoarea tabelara a lui F pentru 1 si N-k grade de libertate este comparata direct cu valorile obtinute.
În cazul problemei de fata, gradele de libertate ale lui F sunt 1 si 20 (24-4), iar valorile tabelare sunt 4,35 pentru p=.05 si 8,10 pentru p=.01.
Deoarece contrastele ortogonale sunt independente, rezultatele pot fi comparate independent (individual). Se observa ca F1 si F2 au valori mai mari decât cele tabelare, ca urmare ipoteza nula este respinsa în cazul lor. Aceasta înseamna ca mediile grupelor 1 si 4 difera semnificativ statistic. La fel si mediile dintre grupele 2 si 3.
Prima situatie valideaza presupozitiile cercetarii în sensul ca persoanele care interactioneaza mai frecvent (variabila independenta) cu cei de etnie rroma vor avea o atitudine mai toleranta fata de acestia. În acest sens se recomanda grupe de lucru mixte, pentru a spori experienta interculturala si interetnica a populatiei majoritare.
A doua situatie ia în calcul durata de interactiune. Deoarece exista diferente semnificative între grupele 2 si 3 se constata ca lungimea duratei de lucru împreuna (1 sau 2 luni) influenteaza atitudinea subiectilor din populatia majoritara. Cu cât lucreaza mai mult împreuna, cu atât atitudinea fata de etnia rroma devine mai toleranta, iar prejudecatile mai putine.
Ultimul raport F (F3) este mai mic decât valoarea tabelara, ca urmare ipoteza nula nu poate fi respinsa si nu se poate spune ca mediile grupelor implicate în ipoteza a treia ar fi diferite.
Analiza directionala
Analiza contrastelor ortogonale studiate în capitolul anterior poate fi aplicata în conditiile în care variabila independenta din ANOVA este exprimata, fie cantitativ (trepte ale drogurilor de 5mg, 10mg, 15mg s.a.), fie calitativ (terapie cognitiv-comportamentala, centrata pe client si grup de control s.a.).
Când însa, treptele variabilei independente sunt numerice (control, 5mg, 10mg s.a.) sau ordinale, ordonate dupa o anumita logica cum ar fi perioada expunerii (înainte, dupa o luna, dupa doua luni s.a.), putem extinde analiza datelor pentru a examina relatiile functionale dintre aceste trepte si media variabilei dependente pe grupe.
În experimentele cu variabile independente calitative, cercetatorul este interesat sa determine daca exista o diferenta între grupe. În schimb, în experimentele cu variabile independente cantitative, se pot urmari aspecte suplimentare care privesc directia datelor.
Procedurile analizei directionale pornesc de la conditia ca treptele variabilei independente sunt egal distantate, iar numarul de subiecti este egal. Aceasta dubla conditie poate fi încalcata, dar procedeul matematic se complica foarte mult. În cele ce urmeaza, vom respecta conditiile de mai sus.
Exista patru tipuri de directii a datelor: liniara (poate apare în designuri experimentale cu doua sau mai multe grupe); curbilinie (poate apare în designuri experimentale cu trei sau mai multe grupe); exponentiala sau cubica (pot apare în designuri experimentale cu patru sau mai multe grupe); cuartica (pot apare în designuri experimentale cu cinci sau mai multe grupe).
Vom prezenta mai jos graficele celor patru tipuri de directii:
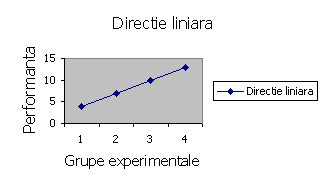
Exemplu: cazul unui design în care grupul 1 este grup de control, grupul 2 urmeaza o data de saptamâna o sedinta de hipnoterapie în vederea reducerii problemelor legate de bulimie. Grupul 3 urmeaza aceeasi terapie, dar de 2 ori pe saptamâna, iar grupul 4 urmeaza de 3 ori pe saptamâna acelasi program.
Din graficul de mai sus, se observa o evolutie liniara, în sensul ca rezultatele sunt cu atât mai bune cu cât creste frecventa sedintelor de terapie.
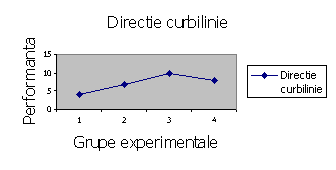
În aceasta situatie se observa ca valorile variabilei dependente scad pentru ultima grupa, ca urmare directia determinata de treptele variabilei independente este pozitiva pâna la un punct, iar apoi descreste.
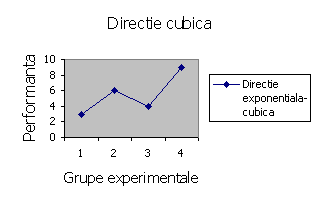
În acest caz, se observa o crestere dozordonata a performantei. Totusi, se remarca rezultatele ultimei grupe ca fiind superioare celorlalte. Se pare ca tratamentul hipnoterapeutic de 3 ore x 3 sedinte pe saptamâna pare a fi cel mai eficient în combaterea acceselor bulimice.
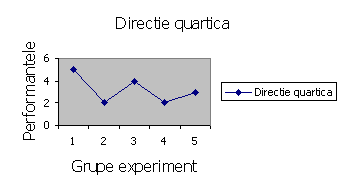
În acest ultim caz se constata o usoara scadere a performantei, dar însotita de cresteri intermitente.
Procedurile utilizate în analiza directionala se bazeaza pe coeficientii numiti coeficienti polinomiali ortogonali pentru a surprinde tendinta de evolutie a datelor variabilei independente în functie de nivelul treptelor variabilei independente, similar comparatiilor planificate ortogonale.
Ca si în cazul contrastelor ortogonale, exista k-1 contraste polinomiale ortogonale. Pentru un design experimental cu trei grupe, putem testa directiile liniare si patratice (curbilinii). Pentru un design cu patru grupe de subiecti putem testa directiile liniara, patratica si cubica. Doar daca exista cinci sau mai multe grupe de subiecti într-un experiment poate fi testata si directia quartica alaturi de celelalte directii.
Coeficientii contrastelor polinomiale ortogonale sunt standardizati însa. Exista un tabel special în care sunt prezentati acesti coeficienti. Voi extrage din tabel doar coeficientii designurilor experimentale cu patru grupe de subiecti. Nu uitati ca treptele variabilei independente trebuie sa fie egal distantate, numerice sau ordinale. Din acest tabel lipsesc coeficientii pentru quartic deoarece acesta poate apare doar de la cinci grupe de subiecti în sus.
K=4 (patru grupe de subiecti) |
||||
| Liniar | -3 |
-1 |
1 |
3 |
| Patratic | 1 |
-1 |
-1 |
1 |
| Cubic | -1 |
3 |
-3 |
1 |
Formula de calcul a lui F pentru analiza directionala este identica cu cea a lui F pentru contraste ortogonale planificate. Doar coeficientii mediilor se modifica, în cazul analizei directionale ei fiind standardizati.
Valorile critice ale lui F se citesc direct din tabelul lui F pentru 1 si N-k grade de libertate.
Daca revenim la problema atitudinii fata de rromi, putem calcula analiza directionala deoarece treptele variabilei independente îndeplinesc conditiile necesare utilizarii formulei prezentate aici.
Tabelul datelor necesare calcularii lui F în cazul acesta este:
| Grupa (k=4) | 1 |
2 |
3 |
4 |
| Medie grupa | 6,5 |
8,0 |
11,0 |
11,0 |
| n grupa | 6 |
6 |
6 |
6 |
| Liniara | -3 |
-1 |
1 |
3 |
| Patratica | 1 |
-1 |
-1 |
1 |
| Cubica | -1 |
3 |
-3 |
1 |
Astfel avem:
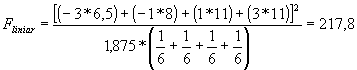
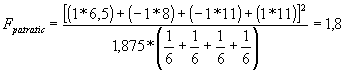
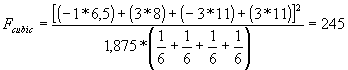
Valoarea tabelara a lui F pentru 1 si 20 (24-4) grade de libertate este 4,35 pentru p=.05, si 8,10 pentru p=.01. Se observa ca doua valori, F liniar si F cubic depasesc acest prag si sunt semnificative pentru analiza directionala realizata.
Acest fapt nu trebuie sa surprinda, deoarece exista posibilitatea ca mai multe directii sa fie semnificative statistic.
OBSERVATIE: Toate metodele prezentate sunt valide atât în cazul ANOVA simpla, cât si în cazul ANOVA cu masuratori repetate. Deoarece MS intragrup pentru ANOVA cu masuratori repetate este mai mica decât MS intragrup pentru ANOVA simpla, din cauza eliminarii MS subiecti se constata ca rezultatele obtinute în cazul ANOVA cu masuratori repetate sunt mai mari si mai des semnificative statistic. Aceasta caracteristica determina ANOVA cu masuratori repetate sa fie un test mai eficient si mai puternic.
Tehnici de comparatii multiple în cazul ANOVA factorial
Daca raportul F a fost semnificativ statistic, vom proceda si în cazul ANOVA factorial la comparatii multiple pentru a observa diferentele dintre diferitele trepte ale variabilelor independente în influentarea variabilei dependente.
Doar în cazul în care avem de a face cu design de tip 2x2 nu sunt necesare asemenea comparatii deoarece un raport F semnificativ, obtinut în urma calculului ANOVA, ne arata ca mediile celor 2 x doua grupe difera.
Dintre metodele prezentate în subcapitolul anterior, ne vom opri la studiul metodei Tukey si a testului efectelor simple. Celelalte metode discutate pot fi utilizate cu mici modificari care sunt asemanatoare cu modificarile metodei Tukey care va fi prezentata în continuare.
Proceduri de comparatie post-hoc
Metoda Tukey
Formula de calcul a metodei Tukey pentru ANOVA factorial este:
![[Image]](pict115.jpg)
Unde: Mi si Mj sunt mediile marginale ale treptelor variabilei independente comparate; MS intra este media patratica a dispersiei intracelule; n marginal este numarul de subiecti cuprinsi în celulele componente ale treptelor comparate.
Ea se aplica pentru cazurile în care efectele principale ale unei sau ambelor variabile independente au fost semnificative statistic si în cazul în care fiecare din aceste variabile are mai mult de doua trepte.
OBSERVATIE: Cea mai importanta conditie pentru a aplica una din metodele de comparatii multiple descrise anterior este ca efectul interactiunii celor doua variabile independente asupra celei dependente sa fie nesemnificativ statistic.
Pentru a întelege utilizarea metodei Tukey în cazul ANOVA factorial vom prezenta o problema care respecta toate aceste conditii.
Un psiholog educational este interesat sa observe daca modul de relationare a profesorului influenteaza baietii si fetele într-un mod diferit. Au fost incluse trei clase în experiment. Într-o clasa, atitudinea profesorului a fost de evitare a elevilor. Profesorul era distant, nu interactiona cu elevii nici în situatia în care acestia rezolvau probleme de matematica mai dificile. Într-o alta clasa, profesorul adopta o atitudine didactogena, potential traumatica, fiind mereu critic în interactiunile sale cu elevii. În cea de a treia clasa profesorul interactiona adecvat cu elevii sai, utilizând frecvent încurajari si laude pentru eforturile depuse de elevi.
Variabila dependenta a fost numarul de erori pe care copiii le-au facut la un test de verificare a cunostintelor dobândite în timpul situatiei experimentale.
Fiind interesati de comparatiile post hoc nu vom mai efectua testul ANOVA, ci ne vom referi direct la aceste metode complementare. Vom porni totusi de la premisa ca efectul interactiunii factorilor sex si atitudine nu a fost semnificativ, spre deosebire de raporturile F pentru fiecare din cei doi factori care pot fi unul sau ambii semnificativi statistic. În plus, datele obtinute în urma calcularii sumelor si mediilor rezultatelor fiecarei celule au fost:
Iata tabelul ANOVA pentru acest caz:
| Sursa dispersiei | SS |
df |
MS |
F |
| Linii –sex | 0,02 |
1 |
0,02 |
0,001 |
| Coloane –atitud. | 227,73 |
2 |
113,86 |
5,72,p<.01 |
| Interactiune LxC | 78,53 |
2 |
39,26 |
1,97 |
| Intracelula | 1074,30 |
54 |
19,89 |
|
| Totala | 1380,58 |
59 |
| Evitare | Critica | Încurajare | ||
| Elevi | S
=169
n=10 M=16,9 |
S
=136
n=10 M=13,6 |
S
=118
n=10 M=11,8 |
M=14,10
N=30 |
| Eleve | S
=146
n=10 M=14,6 |
S
=167
n=10 M=16,7 |
S
=109
n=10 M=10,9 |
M=14,06
N=30 |
| M=15,75
N=20 |
M=15,15
N=20 |
M=11,35
N=20 |
Nu exista un efect semnificativ al interactiunii celor doi factori, de aceea se pot aplica metodele comparative post-hoc prezentate anterior.
De asemenea factorul sex (baieti vs. fete) nu a avut un rol semnificativ în influentarea rezultatelor la proba matematica de performanta. De altfel, chiar daca am fi obtinut un F semnificativ, acesta ar fi fost suficient deoarece existau doar doua trepte ale variabilei.
Problema se pune deci, în a diferentia care grupe au contribuit la obtinerea unui F semnificativ în cazul factorului atitudinea profesorului. Pentru aceasta vom utiliza metoda Tukey pentru a studia care grupe (trepte) ale variabilei independente "atitudine" difera în ce priveste media variabilei dependente.
Vom avea trei comparatii de facut: coloana 1 cu coloana 2; coloana 1 cu coloana 3 si coloana 2 cu coloana 3. Utilizând formula aminitita mai sus avem:
![[Image]](pict116.jpg)
În acelasi mod se calculeaza si celelalte doua valori si vom obtine:
Q13 = (15,75-11,35) / radical din (19,89/20) = 4,41
Q23 = (15,15-11,35) / radical din (19,89/20) = 3,81
Valorile Q obtinute sunt raportate la tabelul lui Q pentru a vedea daca rezultatele obtinute sunt semnificative si sunt capabile sa sesizeze diferentele între grupe. Gradele de libertate ale lui Q se stabilesc tinând cont de doua aspecte (numarul de medii ce trebuie comparate si numarul de grade de libertate pentru dispersia intracelula).
Deoarece exista în acest caz trei medii ce trebuie comparate, iar df pentru intracelula a fost 54, vom cauta valoarea lui Q pentru 3 si 54 grade de libertate. Daca nu este specificata în tabel valoarea dorita, ne vom uita la valoarea precedenta cea mai apropiata. Astfel, deoarece nu este prezentata valoarea lui Q pentru 3 si 54 df, vom urmari Q pentru 3 si 40 grade de libertate, ca fiind valoarea prezentata în tabel care precede cifra dorita de noi.
La un prag de .05 valoarea gasita este 3,44, iar la un prag de .01 este 4,37. Se observa ca valorile gasite de noi sunt semnificative statistic pentru Q13 = 4,41, p<.01 si Q23 = 3,81, p<.05, si nesemnificative pentru Q12 = 0,60, p>.10.
Concluzia ar fi ca atitudinea profesorului de a încuraja elevii s-a dovedit a fi mai eficienta din perspectiva performantei la matematica decât o atitudine evitanta, de neglijare sau decât una mereu critica, potential didactogena.
Metoda efectelor simple
În situatia în care obtinem în ANOVA factorial un raport F semnificativ în ce priveste efectul interactiunii dintre factorii cauzali, nu sunt recomandate metodele comparative post hoc clasice, ci un test al efectelor simple conjugat cu o analiza grafica a interactiunii factorilor, analiza care a fost prezentata când am vorbit despre ANOVA factorial.
Metoda efectelor simple permite analiza diferentelor dintre celulele designului experimental tinând cont de actiunea concomitenta a factorilor (variabilelor independente) ale studiului.
Pentru a aplica aceasta metoda trebuie calculate suma patratelor pentru fiecare linie, respectiv coloana cu ajutorul formulei:
![[Image]](pict117.jpg)
Unde: nc1l este numarul de subiecti din prima celula a unei linii;
ncnl este numarul de subiecti din ultima celula a unei linii;
ntotl este numarul de subiecti ai unei linii indiferent de celula;
S c1lX este suma lui X din prima celula;
S cnlX este suma lui X din ultima celula;
S totlX este suma tuturor X din linia respectiva.
Pentru a întelege mai bine demersul si semnificatia testului efectelor simple, vom apela la o problema amintita în cazul ANOVA factorial.
În experiment, cercetatorul propune subiectilor sa vizioneze un film despre un accident de circulatie. Dupa vizionare le cere subiectilor sa estimeze viteza cu care rulau masinile în momentul accidentului (variabila dependenta). El este interesat de influenta a doua variabile independente.
O prima variabila este data de manipularea experimentatorului: masinile "s-au zdrobit"; "s-au lovit" sau "au circulat". Cea de a doua variabila consta în experienta subiectiilor: soferi si ne-soferi. Avem un model de ANOVA factorial de tip 3x2.
| A1
Zdrobit |
B1 Soferi |
B2 Nesoferi |
S A1(linie)= 189+258=447
S A1 patrat=7623+13644= 21267 Media lui A1 = 44,7 |
||
X |
X² |
X |
X² |
||
| 51 | 2601 | 63 | 3969 | ||
| 45 | 2025 | 57 | 3249 | ||
| 39 | 1521 | 51 | 2601 | ||
| 30 | 900 | 48 | 2304 | ||
| 24 | 576 | 39 | 1521 | ||
| S | 189 | 7623 | 258 | 13644 | |
| Media | 37,8 | 51,6 | |||
| A2
Lovit |
42 | 1764 | 36 | 1296 | S A2(linie)= 174+147=321
S A2 patrat= 6192+4401= 10593 Media lui A2 = 32,1 |
| 39 | 1521 | 30 | 900 | ||
| 33 | 1089 | 30 | 900 | ||
| 33 | 1089 | 27 | 729 | ||
| 27 | 729 | 24 | 576 | ||
| S | 174 | 6192 | 147 | 4401 | |
| Media | 34,8 | 29,4 | |||
| A3
Accident |
33 | 1089 | 36 | 1296 | S (linie)A3 =150+162=312
S A3 patrat = 4536+5310 = 9846 Media lui A3 = 31,2 |
| 33 | 1089 | 33 | 1089 | ||
| 30 | 900 | 36 | 1296 | ||
| 27 | 729 | 30 | 900 | ||
| 27 | 729 | 27 | 729 | ||
| S | 150 | 4536 | 162 | 5310 | |
| Media | 30 | 32,4 | |||
| S B1=189+174+150=513
S B1²=7623+6192+4536 = 18351 Media B1= 34,2 |
S B2=258+147+162=567
S B2²=13644+4401+5310= 23355 Media B2=37,8 |
S Xtotal=1080
S Xtotal² = 41706 Media lui X total = 36 |
|||
Pornind de la aceste date, putem calcula suma patratelor pentru fiecare linie si coloana în parte.
SS linia 1 (A1) este:
![]()
La fel se calculeaza si celelalte linii si coloane si obtinem:
SSA2 = (174 la patrat / 5) + (147 la patrat / 5) – (321 la patrat / 10) = 72,9;
SSA3 = (150 la patrat / 5) + (162 la patrat / 5) – (312 la patrat / 10) = 14,4;
SSB1 = (189 la patrat / 5) + (174 la patrat / 5) + (150 la patrat / 5) – (513 la patrat / 15) = 154,8;
SSB2 = (258 la patrat / 5) + (147 la patrat / 5) + (162 la patrat / 5) – (567 la patrat /15) = 1450,8
Tabelul ANOVA factorial initial arata astfel:
| Sursa dispersiei | SS |
df |
MS |
F |
|
| Linii (A) | 1139,4 |
2 |
569,7 |
12,17 (2,24) p<.01 |
|
| Coloane (B) | 97,2 |
1 |
97,2 |
2,07 (1,24) p>.05 |
|
| Interactiune | 466,2 |
2 |
233,1 |
4,98 (2,24) p<.05 |
|
| Intracelula | 1123,2 |
24 |
46,8 |
||
| Totala | 2826 |
29 |
|||
Pentru a observa efectele simple pe baza acestor date, tabelul sumar ANOVA trebuie diferentiat pe linii si coloane deoarece formula de calcul a lui F în cazul efectelor simple este:
![[Image]](pict119.jpg)
Pentru a calcula media patratica pentru MS efect simplu trebuie sa stabilim gradele de libertate ale acestora. Gradele de libertate pentru linii sunt egale cu numarul de coloane care le întretaie minus unu (c-1), care pentru problema de fata este 1 (2-1), iar pentru coloane este egal cu numarul de linii cu care se intersecteaza minus 1 (l-1), în cazul de fata 2 (3-1).
Ca urmare, tabelul sumar ANOVA dezvoltat pentru studierea efectelor simple devine:
| Sursa dispersiei | SS |
df |
MS |
F |
Prag p |
Linii (A) |
1139,4 |
2 |
569,7 |
12,17(2,24) |
<.01 |
| A – coloana 1 | 154,8 |
2 |
77,4 |
1,65 |
|
| A – coloana 2 | 1450,8 |
2 |
725,4 |
15,50(4,78) |
<.025 |
Coloane (B) |
97,2 |
1 |
97,2 |
1,24(2,07) |
|
B – linia 1 |
476,1 |
1 |
476,1 |
10,17(7,19) |
<.017 |
B – linia 2 |
72,9 |
1 |
72,9 |
1,55 |
|
B – linia 3 |
14,4 |
1 |
14,4 |
0,30 |
|
| Interactiune | 466,2 |
2 |
233,1 |
4,98(2,24) |
<.05 |
| Intracelula 1123,2 | 24 |
46,8 |
|||
| Totala | 2826 |
29 |
|||
Pentru a afla daca valorile F pentru efecte simple sunt semnificative vom consulta acelasi tabel de distributie F. Totusi, în acest caz intervine o modificare a valorii lui alfa pentru a pastra constanta eroarea experimentului.
Astfel, va trebui mai întâi sa împartim nivelul alfa (.05) la numarul de linii respectiv coloane. Pentru problema de fata vom obtine a =.017 pentru linii si a =.025 pentru coloane (exista trei linii si doua coloane în problema data drept model).
Deoarece nu exista trecute în tabel valori F pentru alfa de .017 sau .025 acestea vor fi calculate dupa urmatorul algoritm:
0,05 – 0,017 = 0,033
7,82 – 4,26 = 3,56
Dupa aceasta vom afla valoarea lui F tabelar pentru aceasta situatie:
F tab. = 4,26 + (.033 / .04)*3,56 = 7,19
0,05 – 0,01 = 0,04
0,05 – 0,025 = 0,025
5,61 – 3,40 = 2,21
Valoarea lui F tabelar pentru efectele simple din coloane va fi:
F tab. = 3,40 + (.025 / .04)*2,21 = 4,78
În urma compararii acestor date se observa doua efecte simple semnificative pentru F A-coloana 2, unde s-a obtinut F(2,24) = 15,50, p<.025 (4,78), respectiv F A-linia 1, unde am obtinut F(1,24) = 10,17, p<.017 (7,19). Interpretarea acestor efecte semnificative se face astfel:
I. TEHNICI STATISTICE: Statistica descriptiva,
Studiul corelational, Metode
de comparatie, Tabele,
Formule si raspunsuri la intrebari,
Bibliografie recomandata
II. APLICATII STATISTICE:
Baze de date - Exemple
III. TESTE
IV. LINK-URI RECOMANDATE